|
|
|
|
|
§ 9. Сложение скоростей и переход в другую систему отсчёта при движении на плоскости
Переход в другую систему отсчётаНа рисунке 9.4 схематически изображено положение двух кораблей в море и показаны их скорости Может ли произойти столкновение этих кораблей, если они будут продолжать следовать своими курсами? А если нет, то каким будет минимальное расстояние dmin. между ними?
Если рассматривать движение кораблей в системе отсчёта, связанной с Землёй, ситуация представляется непростой: надо следить одновременно за двумя кораблями, не пропустив момент наибольшего их сближения. Однако эта ситуация значительно упрощается, если перейти в систему отсчёта, связанную с любым из кораблей — например, с кораблём 2 (рис. 9.5).
В этой системе отсчёта корабль 2 покоится, поэтому надо следить за движением только одного корабля — корабля 1. Чтобы найти его скорость
В правой верхней части рисунка 9.5 показано, как графически найти скорость В системе отсчёта, связанной с кораблём 2, корабль 1 движется вдоль прямой, параллельной его скорости Мы видим, что кораблям, к счастью, столкновение не грозит. А проведя перпендикуляр из положения корабля 2 к красному пунктиру, мы найдём и минимальное расстояние между кораблями dmin.
Связанную с автобусом систему отсчёта называем далее для краткости «система А». а) Перенесите рисунок в тетрадь и найдите графически скорость такси в системе А. б) Начертите траекторию движения такси в системе А. в) Найдите модуль скорости такси в системе А. г) Найдите графически и аналитически наименьшее расстояние между такси и автобусом. П о д с к а з к а. Воспользуйтесь подобием треугольников скоростей и перемещений в системе А.
|
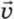1 и 
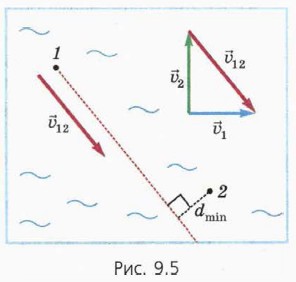
6. На рисунке 9.6 изображено положение автобуса (А) и такси (Т) в некоторый момент времени и обозначены их скорости. Две клетки соответствуют 100 м или
10 м/с.
|
|