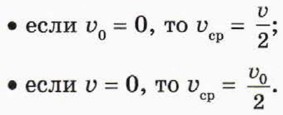Главная >> Физика 10 класс. Часть 1. Генденштейн. Дик

§ 10. «Секреты» прямолинейного равноускоренного движения

Средняя скорость

Продолжим исследование прямолинейного равноускоренного движения, начатое в § 6.

Напомним (см. § 6), что при прямолинейном движении в одном направлении путь I численно равен площади фигуры, заключённой под графиком зависимости υ(t).

Используя этот факт, докажем, что в этом случае средняя скорость равна среднему арифметическому начальной и конечной скорости:

Из определения средней скорости следует, что

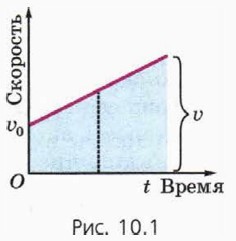
Фигура, заключённая под графиком зависимости υ(t), является в данном случае трапецией с основаниями υ₀ и υ (рис. 10.1). Её площадь, равную l, можно выразить как произведение средней линии (она показана пунктиром) на высоту. Средняя линия данной трапеции равна полусумме её оснований υ и υ₀, а высота равна t. Поэтому получаем:

Левые части уравнений (2) и (3) одинаковы. Следовательно, их правые части равны, откуда и следует формула (1).

1. Начальная скорость автомобиля на участке равна 50 км/ч, а конечная — 70 км/ч. Время движения на участке равно 1 мин. Чему равна длина участка, если автомобиль двигался равноускоренно?

Отметим полезные частные случаи применения формулы для средней скорости равноускоренного движения:

Если движение тела не является равноускоренным, то его средняя скорость может быть и не равна среднему арифметическому начальной и конечной скорости!

Окончание >>>