Пути, проходимые за последовательные равные промежутки времени

6. Галилей доказал, что при прямолинейном равноускоренном движении без начальной скорости пути, проходимые телом за последовательные равные промежутки времени, относятся как последовательные нечётные числа:

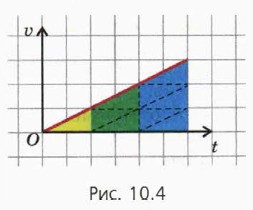
l₁ : l₂ : l₃ = 1 : 3 : 5... .

Воспользовавшись рисунком 10.4, докажите это утверждение.

Может быть, кто-то из вас вспомнит, что для свободного падения без начальной скорости такой результат уже был получен (см. задачу 5 из § 7).

А как обобщается эта красивая теорема (теоремой её назвал сам Галилей) на случай, когда начальная скорость тела не равна нулю?

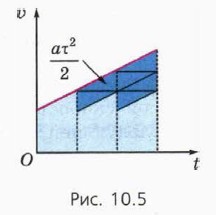
7. Объясните, почему для тела, движущегося прямолинейно равноускоренно в одном направлении, пути, проходимые за последовательные равные промежутки времени продолжительностью τ каждый, образуют арифметическую прогрессию:

l₂ = l₁ + Δ, l₃ = l₁ + 2Δ, ...,

где Δ = аτ² (а — ускорение тела).

П о д с к а з к а. Воспользуйтесь рисунком 10.5. 8

8. В первую секунду наблюдения движущийся равноускоренно автомобиль проехал 10 м, а во вторую — 12 м. Наблюдение длилось 5 с. Попробуйте ответить на следующие вопросы устно.

а) Какое расстояние автомобиль проехал за третью, четвёртую и пятую секунды?

б) С каким ускорением двигался автомобиль?

в) Чему равна начальная скорость автомобиля?