|
|
|
|
|
|
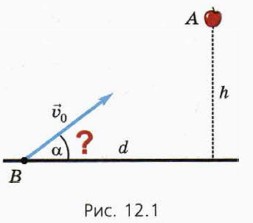
§ 12. Относительное движение брошенных тел. Отскок от наклонной плоскости Относительное движение брошенных телПусть в некоторый момент (t = 0) из точки А на высоте h начинает падать яблоко (рис. 12.1). Лежащий на траве юный стрелок в тот же момент стреляет из пружинного пистолета, намереваясь попасть «в яблочко». Пистолет находится в точке В на расстоянии d от вертикали, вдоль которой падает яблоко, а скорость пули по модулю равна υ0.
1) Под каким углом α к горизонту надо направить пулю? 2) В какой момент времени пуля попадёт в яблоко? Найдём сначала ответы на эти вопросы уже знакомым нам способом. Введём систему координат с началом в точке В, ось х направим по горизонтали вправо, а ось у — вверх. Запишем, как зависят от времени координаты пули и яблока, и учтём, что в момент попадания пули в яблоко их координаты совпадают.
Эта удивительно простая формула утверждает, что целиться надо точно в яблочко — так, будто ни пуля, ни яблоко не чувствуют притяжения Земли! Для того чтобы пуля попала в яблоко, значение имеет (казалось бы) только направление её начальной скорости.
Здесь П о д с к а з к а. Воспользуйтесь тем, что Формула (2) тоже замечательна своей простотой: как будто бы яблоко и правда замерло на месте в ожидании пули, а пуля летела к яблоку, не чувствуя земного притяжения! Найдём теперь физическую разгадку этой «простоты» и покажем, как можно было найти угол а и время полёта устно. Поскольку яблоко и пуля движутся с ускорением свободного падения
Перейдём в систему отсчёта, связанную с яблоком. Скорость яблока в этой системе отсчёта остаётся равной нулю, а скорость пули относительно яблока
Итак, до попадания в яблоко пуля движется относительно яблока с постоянной скоростью
|
|
|



 1. Объясните, почему пуля может попасть в яблоко при условии, что
1. Объясните, почему пуля может попасть в яблоко при условии, что


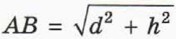 — расстояние между пулей и яблоком в начальный момент.
— расстояние между пулей и яблоком в начальный момент.
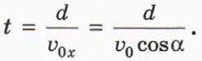
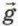 , их скорости в момент времени t в векторном виде выражаются формулами
, их скорости в момент времени t в векторном виде выражаются формулами
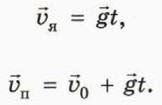
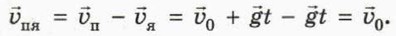
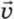 0, то есть прямолинейно и равномерно!
0, то есть прямолинейно и равномерно!