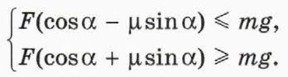|
|
|
|
|
|
§ 20. Движение по горизонтали и вертикали Движение по вертикалиПусть брусок массой m прижимают к стене1 силой 1 Здесь и далее будем подразумевать вертикальную стену.
Если начальная скорость бруска равна нулю, то есть три возможности: брусок может — начать двигаться вверх; — начать двигаться вниз; — остаться в покое. Если брусок начнёт двигаться, то на него будет действовать сила трения скольжения, а если он останется в покое, то на него будет действовать сила трения покоя.
F(cos α — μ sin α) > mg. П о д с к а з к а. В таком случае на брусок действует сила трения скольжения, направленная вниз.
E(cos α + μ sin α) < mg. П о д с к а з к а. Сила трения скольжения направлена вверх.
П о д с к а з к а. Выясните, начнёт ли брусок двигаться. И если начнёт, то в каком направлении.
|
|
|



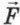 , направленной под углом а к вертикали (рис. 20.4). Коэффициент трения между бруском и стеной равен μ.
, направленной под углом а к вертикали (рис. 20.4). Коэффициент трения между бруском и стеной равен μ.
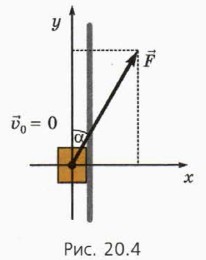
 18. Объясните, почему брусок будет двигаться вверх, если
18. Объясните, почему брусок будет двигаться вверх, если