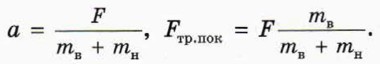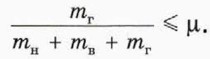Главная >> Физика 10 класс. Часть 1. Генденштейн. Дик

§ 24. Движение системы тел. Учёт трения между телами системы

Тела в начальном состоянии покоятся друг относительно друга (окончание)

13. Объясните, почему, когда бруски движутся как единое целое, их (общее) ускорение а и модуль действующей на каждый брусок силы трения покоя F_{тр. пок} выражаются формулами

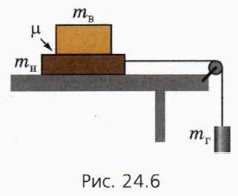
Рассмотрим теперь пример, когда приложена к нижнему бруску.

Пусть на гладком горизонтальном столе лежит брусок массой m_Н, а на нём — брусок массой m_В (рис. 24.6). Коэффициент трения между брусками μ. К нижнему бруску привязана лёгкая нерастяжимая нить, переброшенная через блок, а к нити подвешен груз массой m_Г. Как будут двигаться тела?

В этой ситуации тоже есть две возможности:

1) бруски могут начать двигаться друг относительно друга;

2) бруски могут начать двигаться как единое целое.

На этот раз проще начать со второй возможности, потому что, когда бруски движутся как единое целое, мы можем рассматривать систему, состоящую только из двух тел — объединённого бруска массой М = m_В + m_Н и груза массой m_Г.

14. С каким ускорением движутся бруски как единое целое?

15. С каким максимально возможным ускорением могут двигаться бруски как единое целое?

П о д с к а зк а. Ускорение верхнему бруску сообщает сила трения покоя, которая не превышает силу трения скольжения.

16. Объясните, почему бруски движутся как единое целое, если выполнено соотношение

Если это соотношение не выполнено, то бруски будут двигаться порознь. Ускорение верхнему бруску сообщает в таком случае сила трения скольжения, равная по модулю μm_Вg. Такая же по модулю, но противоположно направленная сила трения скольжения действует на нижний брусок.

17. Каковы ускорения брусков, если они движутся друг относительно друга?

18. На гладком горизонтальном столе лежит брусок массой m_Н = 0,5 кг, а на нём — другой брусок массой m_В = 0,3 кг (см. рис. 24.6). К нижнему бруску привязана лёгкая нерастяжимая нить, переброшенная через блок, а к нити подвешен груз массой m_Г = 0,2 кг. В начальный момент бруски покоятся.

а) При каком наименьшем коэффициенте трения μ_min между брусками они будут двигаться как единое целое?

б) С каким ускорением (ускорениями) движутся бруски при коэффициенте трения между ними 0,5?

в) С каким ускорением (ускорениями) движутся бруски, если коэффициент трения между ними равен 0,1?

<<< К началу