|
|
|
|
|
|
§ 27. Реактивное движение. Освоение космоса Реактивное движение (окончание)Выберем инерциальную систему отсчёта, в которой в начальный момент ракета покоилась, причём её двигатель был выключен. Пусть при включении двигателя из сопла ракеты вылетела порция газа массой mг со скоростью Согласно закону сохранения импульса суммарный импульс ракеты и газа в этой системе отсчёта остался равным нулю. Поэтому mр Здесь mр — масса ракеты (оставшаяся после выброса порции газа),
Ракеты используют для запуска искусственных спутников Земли, обслуживания орбитальных станций, межпланетных полётов. В головной части ракеты расположена кабина космонавтов. В начале полёта на эту часть приходится всего несколько процентов от общей массы ракеты. Основную же массу ракеты в начале полёта составляет запас топлива. В современных ракетах скорость вылетающего газа (относительно ракеты) составляет несколько километров в секунду (в несколько раз больше скорости пули). Как следует из соотношения (1), для того чтобы даже при такой огромной скорости вылетающего газа ракета приобрела первую космическую скорость (около 8 км/с), необходимо, чтобы масса топлива в несколько раз превышала массу полезного груза. Однако весь газ нельзя выбрасывать из ракеты сразу! Дело в том, что ускорение ракеты было бы при этом настолько большим, что возникшую перегрузку не смогли бы выдержать не только космонавты, но и приборы. Почему ракеты делают многоступенчатыми?Чтобы избежать больших перегрузок, ракета должна разгоняться в течение достаточно длительного промежутка времени. А при длительном разгоне вылетающий из сопла ракеты газ должен разгонять не только саму ракету, но и весь огромный запас топлива, который ракета несёт в своём корпусе. В результате расход топлива многократно увеличивается. Например, чтобы без чрезмерных перегрузок разогнать ракету до первой космической скорости, масса топлива должна в десятки раз превышать массу полезного груза. Поэтому ракету делают многоступенчатой. Первая и вторая ступени ракеты представляют собой ёмкости с топливом, камерами сгорания и соплами. Когда топливо, содержащееся в первой ступени, сгорает, она отделяется от ракеты, в результате чего масса ракеты значительно уменьшается. Затем то же происходит со второй ступенью, после чего включаются двигатели третьей ступени, завершающие разгон ракеты до расчётной скорости. Расчёт передаваемого ракете импульсаРассмотрим несколько упрощённый пример расчёта скорости движения ракеты.
а) Чему равен импульс выброшенного за 1 с газа в инерциальной системе отсчёта, в которой ракета в начальный момент покоилась? б) Чему равно изменение импульса ракеты за 1 с в той же системе отсчёта? в) Какая сила действовала на ракету со стороны газа? г) Чему равно ускорение ракеты в упомянутой системе отсчёта?
|
|
|



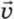 г относительно выбранной системы отсчёта.
г относительно выбранной системы отсчёта.
 1. Докажите, что изменение скорости ракеты прямо пропорционально массе выброшенного газа и его скорости относительно ракеты и обратно пропорционально массе ракеты.
1. Докажите, что изменение скорости ракеты прямо пропорционально массе выброшенного газа и его скорости относительно ракеты и обратно пропорционально массе ракеты.