|
|
|
|
|
§ 3. Сложение скоростей и переход в другую систему отсчёта при движении вдоль одной прямой Переход в другую систему отсчёта (окончание)
Выведем общую формулу для нахождения скорости тела в системе отсчёта, связанной с другим телом. Воспользуемся для этого правилом сложения скоростей. Напомним, что оно выражается формулой
где Перепишем формулу (1) в виде
где Эта формула позволяет найти скорость
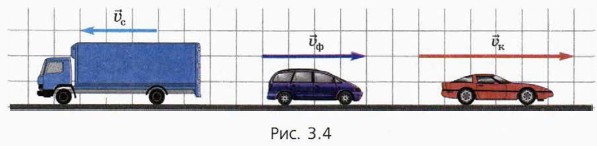
Найдите: а) скорость синего и фиолетового автомобилей в системе отсчёта, связанной с красным автомобилем; б) скорость синего и красного автомобилей в системе отсчёта, связанной с фиолетовым автомобилем; в) скорость красного и фиолетового автомобилей в системе отсчёта, связанной с синим автомобилем; г) какая (какие) из найденных скоростей наибольшая по модулю? наименьшая? <<< К началу Вопросы и задания >>>
|
|
|



 6. По прямой дороге со скоростью 1м/с идёт пешая колонна длиной 200 м. Находящийся во главе колонны командир посылает всадника с поручением к замыкающему. Через сколько времени всадник вернётся обратно, если он скачет со скоростью 9 м/с?
6. По прямой дороге со скоростью 1м/с идёт пешая колонна длиной 200 м. Находящийся во главе колонны командир посылает всадника с поручением к замыкающему. Через сколько времени всадник вернётся обратно, если он скачет со скоростью 9 м/с?
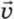 1 =
1 =