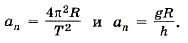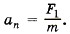|
|
|
|
|
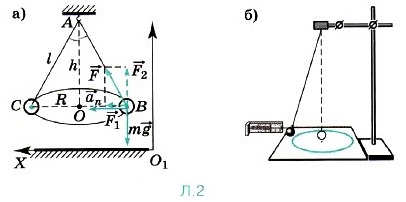
Лабораторная работа № 1 Изучение движения тела по окружностиЦель работы Определить центростремительное ускорение шарика при его равномерном движении по окружности. Теоретическая часть Эксперименты проводятся с коническим маятником. Небольшой шарик движется по окружности радиусом R. При этом нить АВ, к которой прикреплён шарик, описывает поверхность прямого кругового конуса. Из кинематических соотношений следует, что аn = ω2R = 4π2R/T2. На шарик действуют две силы: сила тяжести m
Модуль составляющей F1 можно определить, пользуясь подобием треугольников ОАВ и F1FB: F1/R = mg/h (|m Сопоставим все три выражения для аn: аn = 4 π2R/T2, аn =gR/h, аn = F1/m и убедимся, что числовые значения центростремительного ускорения, полученные тремя способами, примерно одинаковы. Оборудование Штатив с муфтой и лапкой, лента измерительная, циркуль, динамометр лабораторный, весы с разновесами, шарик на нити, кусочек пробки с отверстием, лист бумаги, линейка. Порядок выполнения работы 1. Определите массу шарика на весах с точностью до 1 г. 2. Нить проденьте сквозь отверстие в пробке и зажмите пробку в лапке штатива (рис. Л.2, б). 3. Начертите на листе бумаги окружность, радиус которой около 20 см. Измерьте радиус с точностью до 1 см. 4. Штатив с маятником расположите так, чтобы продолжение нити проходило через центр окружности. 5. Взяв нить пальцами у точки подвеса, вращайте маятник так, чтобы шарик описывал такую же окружность, как и начерченная на бумаге. 6. Отсчитайте время, за которое маятник совершает заданное число (например, в интервале от 30 до 60) оборотов. 7. Определите высоту конического маятника. Для этого измерьте расстояние по вертикали от центра шарика до точки подвеса (считаем h ≈ l). 8. Найдите модуль центростремительного ускорения по формулам
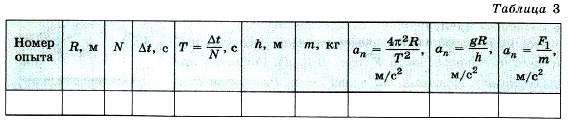
9. Оттяните горизонтально расположенным динамометром шарик на расстояние, равное радиусу окружности, и измерьте модуль составляющей Затем вычислите ускорение по формуле 10. Результаты измерений (в СИ) и вычислений занесите в таблицу 3.
Сравнивая полученные три значения модуля центростремительного ускорения, убеждаемся, что они примерно одинаковы.
|
|
|



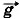 и сила натяжения нити
и сила натяжения нити 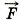 (рис. Л.2, а). Согласно второму закону Ньютона m
(рис. Л.2, а). Согласно второму закону Ньютона m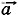 = m
= m