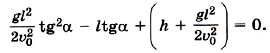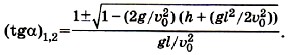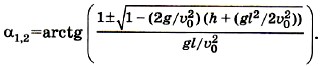|
|
|
|
|
Примеры решения задач Движение с постоянным ускорением свободного падения: Движение с постоянным ускорением свободного падения (продолжение)В этом случае движение шарика будет описываться кинематическими уравнениями
При сделанном выборе начала координат и направлений осей ОХ и OY имеем х0 = 0, у0 = |ОА|, υ0x = υ0, υ0y = 0, ах = О, ау = -g. Поэтому х = υ0t,
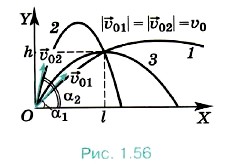
Задача 3. Футболист, находясь от ворот на расстоянии l, ударяет по мячу, и мяч летит с начальной скоростью υ0 и пролетает мимо, едва коснувшись верхней планки ворот. Высота ворот h. Определите, под каким углом начал лететь мяч, после того как футболист ударил по нему. Р е ш е н и е. Выбрав систему координат так, как показано на рисунке 1.56, и начало координат в точке удара по мячу, отметим, что координаты мяча в момент касания верхней планки ворот будут х = l, у = h.
Запишем уравнения движения мяча вдоль осей ОХ и OY: х = (υ0cosα)t;
Выразив из первого уравнения время и подставив его во второе, получим
Тогда у верхней планки ворот
Решив его, найдём Тогда значения угла Оба значения имеют смысл. Кроме этого, если (g/υ20)(h + gl2/2υ20) = = 1/2, то мяч касается планки в наивысшей точки траектории. На рисунке 1.56 показаны три возможные траектории полёта мяча.
|
|
|



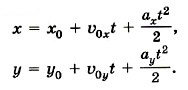
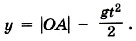 Спустя время t1 = 1,5 с координаты шарика будут равны:
Спустя время t1 = 1,5 с координаты шарика будут равны:
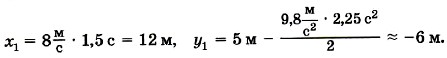
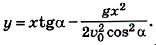
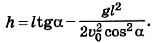 Мы получили тригонометрическое уравнение. Произведя замену 1/(cos2α) = 1 + tg2α и выполнив необходимые преобразования, получим квадратное уравнение относительно tgα:
Мы получили тригонометрическое уравнение. Произведя замену 1/(cos2α) = 1 + tg2α и выполнив необходимые преобразования, получим квадратное уравнение относительно tgα: