|
|
|
|
|
Глава 1. Кинематика точки и твёрдого тела Первый закон Ньютона
Однако, помимо инерциальных систем отсчёта, есть и другие, в которых тело имеет ускорение даже в том случае, когда на него другие тела не действуют. В качестве примера рассмотрим систему отсчёта, связанную с автобусом. При равномерном движении автобуса пассажир может не держаться за поручень, действие со стороны автобуса компенсируется взаимодействием с Землёй. При резком торможении автобуса стоящие в проходе пассажиры падают вперёд, получая ускорение относительно стенок автобуса (рис. 2.6). Однако это ускорение не вызвано какими-либо новыми воздействиями со стороны Земли или автобуса непосредственно на пассажиров. Относительно Земли пассажиры сохраняют свою постоянную скорость, но автобус начинает двигаться с ускорением, и пассажиры относительно него также движутся с ускорением. Ускорение появляется вследствие того, что движение их рассматривается относительно тела отсчёта (автобуса), движущегося с ускорением.
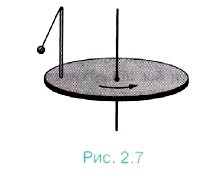
Рассмотрим маятник, находящийся на вращающемся диске (рис. 2.7). Нить маятника отклонена от вертикали, хотя сам он неподвижен относительно диска. Натяжение нити не может быть скомпенсировано силой притяжения к Земле. Следовательно, отклонение маятника нельзя объяснить только его взаимодействием с телами.
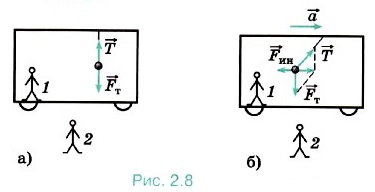
Рассмотрим ещё один маятник, находящийся в неподвижном вагоне. Нить маятника вертикальна (рис. 2.8, а). Шарик взаимодействует с нитью и Землёй, сила натяжения нити равна силе тяжести. С точки зрения пассажира в вагоне и человека, стоящего на перроне, шарик находится в равновесии вследствие того, что сумма сил, действующих на него, равна нулю.
Как только вагон начинает двигаться с ускорением, нить маятника отклоняется (шарик по инерции стремится сохранить состояние покоя). С точки зрения человека, стоящего на перроне, ускорение шарика должно быть равно ускорению вагона, так как нить не разрывается и шарик движется вместе с вагоном. Шарик по-прежнему взаимодействует с теми же телами, сумма сил этого взаимодействия должна быть отлична от нуля и определять ускорение шарика. С точки зрения пассажира, находящегося в вагоне, шарик неподвижен, следовательно, сумма сил, действующих на шарик, должна быть равна нулю, однако на шарик действуют те же силы — натяжения нити и сила Рис. 2.8 тяжести. Значит, на шарик (рис. 2.8, б) должна действовать сила В неинерциальных системах отсчёта основное положение механики о том, что ускорение тела вызывается действием на него других тел, не выполняется.
|
|
|



 Приведите примеры инерциальных и неинерциальных систем отсчёта.
Приведите примеры инерциальных и неинерциальных систем отсчёта.

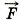 ин, которая определяется тем, что система отсчёта, связанная с вагоном, неинерциальная. Эту силу называют силой инерции (см. рис. 2.8, б).
ин, которая определяется тем, что система отсчёта, связанная с вагоном, неинерциальная. Эту силу называют силой инерции (см. рис. 2.8, б).