Главная >> Физика 10 класс. Мякишев

Глава 1. Кинематика точки и твёрдого тела

§ 3. Траектория. Путь. Перемещение

С какими векторными величинами вы встречались на уроках физики?

Чем отличаются векторные величины от скалярных?

Запомни Линия, по которой движется точка в пространстве, называется траекторией.

В зависимости от формы траектории все движения точки делятся на прямолинейные и криволинейные.

Запомни Если траекторией является прямая линия, движение точки называется прямолинейным, а если кривая — криволинейным.

С верхней полки вагона поезда, движущегося прямолинейно, уронили предмет. Можно ли считать движение предмета прямолинейным в системе отсчёта, связанной с вагоном? в системе отсчёта, связанной с землёй?

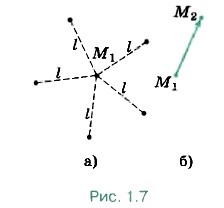
Пусть в какой-то момент времени движущаяся точка занимает положение М₁ (рис. 1.7, а). Как найти её положение спустя некоторый промежуток времени после этого момента?

Допустим, известно, что точка находится на расстоянии l относительно своего начального положения. Сможем ли мы в этом случае однозначно определить новое положение точки? Очевидно, нет, поскольку есть бесчисленное множество точек, которые удалены от точки М₁ на расстояние l. Чтобы однозначно определить новое положение точки, надо ещё знать, в каком направлении от точки М₁ следует отложить отрезок длиной l.

Таким образом, если известно положение точки в какой-то момент времени, то найти её новое положение можно с помощью определённого вектора (рис. 1.7, б).

Запомни Вектор, проведённый из начального положения точки в её конечное положение, называется вектором перемещения или просто перемещением точки.

Поскольку перемещение — величина векторная, то перемещение, показанное на рисунке (1.7, б), можно обозначить

Покажем, что при векторном способе задания движения перемещение можно рассматривать как изменение радиус-вектора движущейся точки.

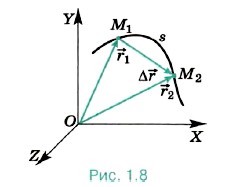
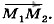
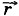Пусть радиус-вектор ₁ задаёт положение точки в момент времени t₁, а радиус-вектор ₂ — в момент времени t₂ (рис. 1.8). Чтобы найти изменение радиус-вектора за промежуток времени Δt = t₂ - t₁, надо из конечного вектора ₂ вычесть начальный вектор ₁. Из рисунка 1.8 видно, что перемещение, совершённое точкой за промежуток времени Δt, есть изменение её радиус-вектора за это время. Следовательно, обозначив изменение радиус-вектора через Δ , можно записать: Δ = ₁ - ₂.

Окончание >>>