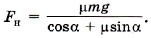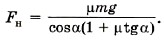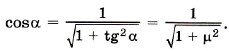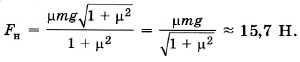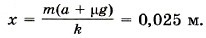|
|
|
|
|
Глава 3. Силы в механике Примеры решения задач по теме «Силы трения»Согласно второму закону Ньютона m В проекциях на оси ОХ и OY уравнение имеет вид mа = Т - mg sinα - Сила трения скольжения Из уравнения (3) получим N = mg cosa. Уравнение (2) перепишем в виде mа = Т - mg sinα - μmg cosα. Ускорение определим из уравнения движения
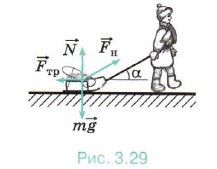
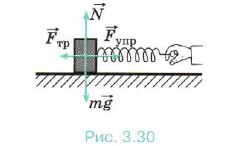
Задача 4. Девочка тянет равномерно по снегу нагруженные санки массой 40 кг. Коэффициент трения санок о снег 0,04. Определите, под каким углом должна быть расположена верёвка, чтобы её натяжение было минимально. Р е ш е н и е. На санки действуют сила натяжения верёвки m
Так как движение по условию равномерное, то ускорение а = 0. Запишем уравнение (1) в проекциях на горизонтальное и вертикальное направления: 0 = Fн cosα - Fтp; (2)
Из уравнения (3) получим N = mg - Fн sinα. Подставив в уравнение (2) выражение для силы трения Fтp = μx(mg - Fн sinα), получим Fн cosα - μx(mg - Fн sinα) = 0. Для силы натяжения имеем Сила натяжения минимальна при максимальном значении суммы cosα + μsinα = ƒ(α). Исследуем функцию на экстремум: ƒ' = -sinα + μcosα = 0. Получим tgα = μ. Тогда Выразим cosa через tgα: Окончательно для силы натяжения получим Задача 5. Брусок массой 5 кг тянут по поверхности стола, взявшись за кольцо динамометра. При этом ускорение тела равно 0,5 м/с2. Жёсткость пружины равна 200 Н/м Определите растяжение пружины. Коэффициент трения бруска о стол 0,05. Р е ш е н и е. На брусок действуют сила тяжести m
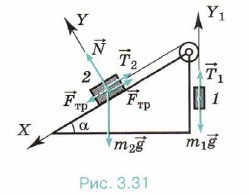
Согласно второму закону Ньютона m В проекции на горизонталь уравнение запишем в виде mа = Fyпp - Fтp. Сила трения Fтp = μN = μmg. Сила упругости Fyпp = -kx. Тогда mа = kx - μmg. Удлинение пружины Задача 6. Два бруска массами m1 = 1 кг и m2 = 3 кг соединены нерастяжимой нитью, перекинутой через блок. Брусок с большей массой находится на наклонной плоскости, угол у основания которой равен 30°, коэффициент трения равен 0,04. Определите ускорение брусков. Р е ш е н и е. На первый брусок действуют сила натяжения нити
|
|
|



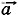 = m
= m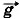 + N +
+ N + 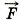 тp +
тp + 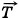 . (1)
. (1)
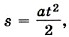 при этом
при этом 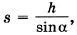
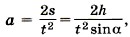
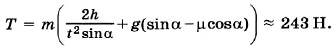
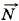 и сила трения
и сила трения