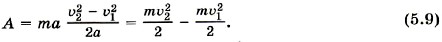|
|
|
|
|
Глава 5. Закон сохранения энергии § 41. Энергия. Кинетическая энергияВспомните, когда мы можем сказать, что у тела есть энергия. Какие физические величины определяют механическую энергию тела? Какие виды механической энергии вы знаете? Если система тел может совершить работу, то мы говорим, что она обладает энергией.
Совершая механическую работу, тело или система тел переходят из одного состояния в другое, в котором их энергия минимальна. Груз опускается, пружина распрямляется, движущееся тело останавливается. При совершении работы энергия постепенно расходуется. Для того чтобы система опять приобрела способность совершать работу, надо изменить её состояние: увеличить скорости тел, поднять тела вверх или деформировать. Для этого внешние силы должны совершить над системой положительную работу. Энергия в механике — величина, определяемая состоянием системы — положением тел или частей тела и их скоростями.
Подсчитаем работу постоянной силы А = F|Δ
Выберем координатную ось ОХ так, чтобы векторы А = FΔx. (5.6) Согласно второму закону Ньютона F = mа. (5.7) Так как точка движется с постоянным ускорением, то изменение её координаты Δх при переходе из начального положения в конечное можно найти по известной нам из кинематики формуле
Подставляя формулы (5.7) и (5.8) в формулу (5.6), получаем
|
|
|



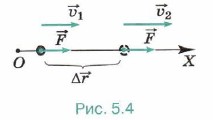
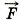 , действующей на материальную точку массой m при его прямолинейном движении. Пусть направление силы совпадает с направлением скорости материальной точки. В этом случае направления вектора перемещения Дс и вектора силы совпадают (рис. 5.4). Поэтому работа силы Δ
, действующей на материальную точку массой m при его прямолинейном движении. Пусть направление силы совпадает с направлением скорости материальной точки. В этом случае направления вектора перемещения Дс и вектора силы совпадают (рис. 5.4). Поэтому работа силы Δ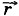 :
:
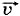 1,
1, 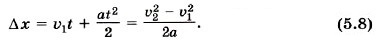
 Повторите кинематику и выведите самостоятельно формулу (5.8).
Повторите кинематику и выведите самостоятельно формулу (5.8).