|
|
|
|
|
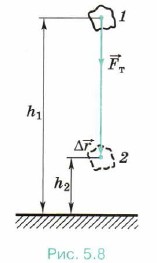
Глава 5. Закон сохранения энергии § 43. Работа силы тяжести и силы упругости. Консервативные силыПо какой формуле можно вычислить работу силы? Что общего между работой силы тяжести и силы упругости? Работа силы тяжести. Вычислим работу силы тяжести при падении тела (например, камня) вертикально вниз. В начальный момент времени тело находилось на высоте hx над поверхностью Земли, а в конечный момент времени — на высоте h2 (рис. 5.8). Модуль перемещения тела |Δ
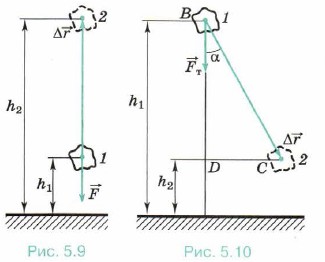
Направления векторов силы тяжести А = | Пусть теперь тело бросили вертикально вверх из точки, расположенной на высоте h1 над поверхностью Земли, и оно достигло высоты h2 (рис. 5.9). Векторы А = |
Если же тело перемещается по прямой так, что направление перемещения составляет угол а с направлением силы тяжести (рис. 5.10), то работа силы тяжести равна: А = | Из прямоугольного треугольника BCD видно, что |BC|cosα = BD = h1 — h2. Следовательно, А = mg(h1 - h2) = mgh1 - mgh2. (5.14) Это выражение совпадает с выражением (5.12).
|
|
|



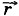 | = h1 - h2.
| = h1 - h2.
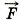 T и перемещения Δ
T и перемещения Δ Предположите, что тело перемещается между точками 1 и 2 (см. рис. 5.10) по ломаной линии. Покажите, что работа силы тяжести и в этом случае определяется выражением (5.13).
Предположите, что тело перемещается между точками 1 и 2 (см. рис. 5.10) по ломаной линии. Покажите, что работа силы тяжести и в этом случае определяется выражением (5.13).