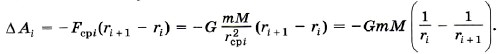|
|
|
|
|
Глава 5. Закон сохранения энергии § 46. Работа силы тяготения. Потенциальная энергия в поле тяготенияВ чём выражается гравитационное взаимодействие тел? Как доказать наличие взаимодействия Земли и, например, учебника физики? В § 43 мы рассмотрели работу силы тяжести и выяснили, что сила тяжести — консервативная сила. Теперь найдём выражение для работы силы тяготения и докажем, что работа этой силы не зависит от формы траектории, т. е. что сила тяготения также консервативная сила. Напомним, что работа консервативной силы по замкнутому контуру равна нулю. Пусть тело массой m находится в поле тяготения Земли. Очевидно, что размеры этого тела малы по сравнению с размерами Земли, поэтому его можно считать материальной точкой. На тело действует сила тяготения
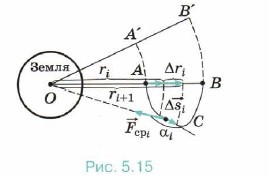
где G — гравитационная постоянная, М — масса Земли, r — расстояние, на котором находится тело от центра Земли. Пусть тело перемещается из положения А в положение В по разным траекториям: 1) по прямой АВ; 2) по кривой АА'В'В; 3) по кривой АСВ (рис. 5.15)
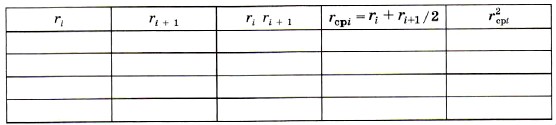
1. Рассмотрим первый случай. Сила тяготения, действующая на тело, непрерывно уменьшается, поэтому рассмотрим работу этой силы на малом перемещении Δri = ri + 1 — ri. Среднее значение силы тяготения равно:
Чем меньше Δri, тем более справедливо написанное выражение r2сpi = riri + 1.
Тогда работу силы Fсpi, на малом перемещении Δri, можно записать в виде
|
|
|



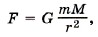
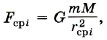 где r2сpi = riri + 1.
где r2сpi = riri + 1.
 Проверьте это утверждение, подставляя разные числа.
Проверьте это утверждение, подставляя разные числа.