|
|
|
|
|
Глава 6. Динамика вращательного движения абсолютно твёрдого тела § 48. Основное уравнение динамики вращательного движенияПовторите основные понятия и соотношения кинематики вращательного движения абсолютно твёрдого тела, изложенные в § 16 главы 1. Угловое ускорениеРанее мы получили формулу, связывающую линейную скорость υ, угловую скорость ω и радиус R окружности, по которой движется выбранный элемент (материальная точка) абсолютно твёрдого тела, которое, вращается относительно неподвижной оси: υ = ωR. Мы знаем, что линейные скорости и ускорения точек твёрдого тела различны. В то же время угловая скорость всех точек твёрдого тела одинакова. Угловая скорость — векторная величина. Направление угловой скорости определяется по правилу буравчика. Если направление вращения ручки буравчика совпадает с направлением вращения тела, то поступательное движение буравчика указывает направление вектора угловой скорости (рис. 6.1).
Однако равномерное вращательное движение встречается довольно редко. Гораздо чаще мы имеем дело с движением, при котором угловая скорость изменяется, очевидно, это происходит в начале и конце движения. Причиной изменения угловой скорости вращения является действие на тело сил. Изменение угловой скорости со временем определяет угловое ускорение.
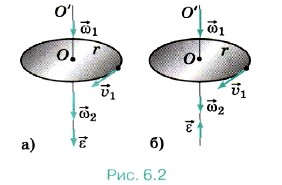
При равноускоренном движении угловое ускорение постоянно и при неподвижной оси вращения характеризует изменение угловой скорости по модулю. При увеличении угловой скорости вращения тела угловое ускорение направлено в ту же сторону, что и угловая скорость (рис. 6.2, а), а при уменьшении — в противоположную (рис. 6.2, б).
Так как угловая скорость связана с линейной скоростью соотношением υ = ωR, то изменение линейной скорости за некоторый промежуток времени Δt равно Δυ =ΔωR. Разделив левую и правую части уравнения на Δt, имеем Если время измерено в секундах, а угловая скорость — в радианах в секунду, то одна единица углового ускорения равна 1 рад/с2 , т. е. угловое ускорение выражается в радианах на секунду в квадрате.
|
|
|



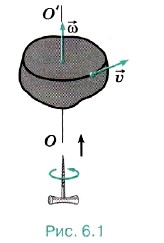
 Bектор угловой скорости — это скользящий вектор. Независимо от точки приложения его направление указывает направление вращения тела, а модуль определяет быстроту вращения,
Bектор угловой скорости — это скользящий вектор. Независимо от точки приложения его направление указывает направление вращения тела, а модуль определяет быстроту вращения,
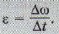
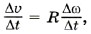 или а = εR, где а — касательное (линейное) ускорение, направленное по касательной к траектории движения (окружности).
или а = εR, где а — касательное (линейное) ускорение, направленное по касательной к траектории движения (окружности).
 Чем различаются два вектора — вектор линейной скорости и вектор угловой скорости.
Чем различаются два вектора — вектор линейной скорости и вектор угловой скорости.