|
|
|
|
|
Глава 1. Кинематика точки и твёрдого тела § 7. Примеры решения задач по теме «Сложение скоростей»При решении задач на эту тему прежде всего надо грамотно выбрать тело отсчёта, с которым связать неподвижную систему координат. Затем выбрать тело отсчёта, движущееся относительно первого, и связать с ним подвижную систему координат. В этих двух системах рассмотреть движение тела и записать закон сложения скоростей. Задача 1. Два поезда движутся равномерно друг за другом. Скорость первого равна 80 км/ч, а скорость второго — 60 км/ч. Определите скорость второго поезда относительно первого. Р е ш е н и е. Обозначим скорость первого поезда относительно земли через
где
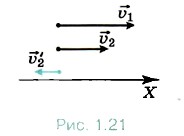
Это сложение скоростей поясняется на рисунке 1.21. Из рисунка видно, что скорость второго поезда относительно первого направлена в сторону, противоположную направлению движения поездов, и второй поезд удаляется от первого. Проекция скорости υ'2 = υ2 - υ1 = -20 км/ч.
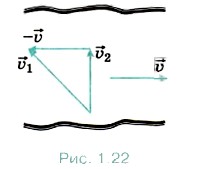
Задача 2. Скорость течения реки υ = 1,5 м/с. Определите модуль скорости υ1 катера относительно воды, если катер движется перпендикулярно к берегу со скоростью υ2 = 2 м/с относительно его. Р е ш е н и е. Согласно закону сложения скоростей (1.9)
Отсюда скорость катера относительно воды
Векторное сложение скоростей
Так как полученный треугольник скоростей прямоугольный, то Задача 3. Самолёт, скорость которого относительно воздуха равна 300 км/ч, летит на север. Внезапно подул северо-западный ветер со скоростью 100 км/ч относительно земли. Определите, под каким углом к направлению на запад лётчик должен направлять самолёт, чтобы продолжать лететь на север, и чему при этом будет равна скорость самолёта относительно земли.
|
|
|



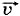 1, а скорость второго поезда — через
1, а скорость второго поезда — через