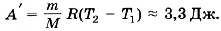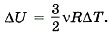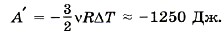|
|
|
|
|
Глава 13. Основы термодинамики § 75. Примеры решения задач по теме: Внутренняя энергия. РаботаДля решения задач нужно уметь вычислять внутреннюю энергию и работу, пользуясь формулами (13.1) и (13.4). Надо ещё иметь в виду, что величины A, Q, ΔU могут быть как положительными, так и отрицательными. Задача 1. Аэростат объёмом V = 500 м3 наполнен гелием под давлением р = 105 Па. В результате солнечного нагрева температура газа в аэростате поднялась от t1 = 10 °С до t2 = 25 °С. На сколько увеличилась внутренняя энергия газа? Р е ш е н и е. Гелий является одноатомным газом, поэтому его внутренняя энергия определяется формулой (13.1). При температуре Т1 эта энергия равна
Масса гелия неизвестна, но её можно выразить с помощью уравнения Менделеева—Клапейрона через начальную температуру, давление и объём газа:
Задача 2. В цилиндре под тяжёлым поршнем находится углекислый газ (М = 0,044 кг/моль) массой m = 0,20 кг. Газ нагревается на ΔТ = 88 К. Какую работу он при этом совершает? Р е ш е н и е. Газ расширяется при некотором постоянном давлении р, которое создаётся атмосферой и поршнем. В этом случае работа газа А' = p(V2 - V1), где V1 и V2 — начальный и конечный объёмы газа. Используя уравнение Менделеева—Клапейрона, выразим произведения pV2 и pV1 через
Задача 3. Чему равна работа, совершённая газом в количестве 3 моль при сжатии, если температура увеличилась на 100 К? Потери тепла не учитывайте. Р е ш е н и е. При сжатии внешняя сила совершает положительную работу, за счёт которой происходит изменение внутренней энергии и соответственно температуры газа, т. е. А = ΔU. Изменение внутренней энергии
Работа, совершённая силой давления газа:
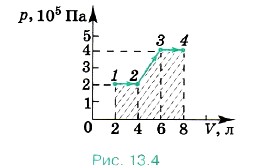
Задача 4. На рисунке 13.4 показана зависимость давления газа от объёма при его переходе из состояния 1 в состояние 4. Определите работу газа.
|
|
|



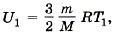 а при температуре Т2 равна
а при температуре Т2 равна 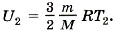 Изменение энергии равно:
Изменение энергии равно:
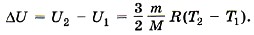
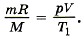 Подставляя значение
Подставляя значение 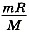 в уравнение для изменения энергии, получаем
в уравнение для изменения энергии, получаем
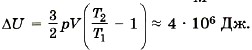
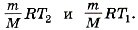 Тогда
Тогда