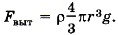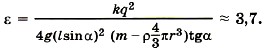|
|
|
|
|
Глава 14. Электростатика Примеры решения задач по теме: Закон Кулона (продолжение)Решим полученную систему уравнений относительно двух неизвестных qx и lx. Из первого уравнения выразим |qx|: Получим уравнение Решением этого уравнения, удовлетворяющим физическому смыслу, является lx - 1 м. Подставив это значение в формулу для |qx|, получим |qx| = |q2| = 8 • 10-4 Кл, или qx = -8 • 10-4 Кл. Задача 4. Два заряженных шарика, находящиеся друг от друга на расстоянии r = 90 см и помещённые в керосин, притягиваются друг к другу с силой F = 80 Н. Определите заряды шариков, если сумма их зарядов q = 4 • 10-5 Кл. Относительная диэлектрическая проницаемость керосина ε = 2. Р е ш е н и е. Так как шарики притягиваются, то их заряды противоположны по знаку. Предположим, что заряд первого шарика положителен и равен q1, а второго отрицателен и равен q2. Согласно условию задачи q1 + q2 = q, или q1 - |q2| = q. (1) По закону Кулона сила притяжения зарядов равна:
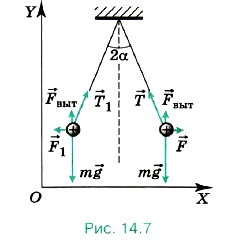
Уравнения (1) и (2) — система двух уравнений относительно двух неизвестных q1 и |q2|. Выразив из уравнения Относительно модуля заряда |q2| получим уравнение Отсюда Таким образом, q2 = -10-4 Кл, a q1 = 1,4 • 10-4 Кл. Задача 5. Два одинаковых небольших одноимённо заряженных шарика радиусом 1 см, массой 10 г и зарядом 4 • 10-6 Кл подвешены в одной точке на двух нитях длиной 1 м в жидком диэлектрике. Плотность диэлектрика ρ = 800 кг/м3. Определите относительную диэлектрическую проницаемость диэлектрика ε, если угол между нитями 2α = 60°. Р е ш е н и е. На каждый шарик действуют сила тяжести, сила натяжения нити, выталкивающая сила и сила Кулона (рис. 14.7).
Условия равновесия шариков m В проекциях на оси координат для правого шарика запишем: на ось OX: -Tsinα + F = 0; на ось ОY: -mg + Tcosα + Fвыт = 0. Выразив силу Т из этих уравнений и приравняв правые части полученных выражений, найдём
При этом сила Кулона Подставим эти выражения в уравнение (1) и найдём диэлектрическую проницаемость:
|
|
|



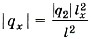 — и подставим во второе.
— и подставим во второе.
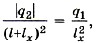 или
или 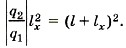 Подставим значения зарядов:
Подставим значения зарядов: 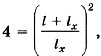 или
или 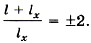

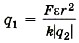 и подставив в уравнение (1), получим
и подставив в уравнение (1), получим 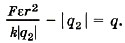
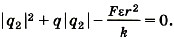
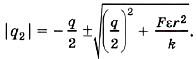 Модуль числа всегда положителен, поэтому оставляем один корень |q2| ≈ 10-4 Кл.
Модуль числа всегда положителен, поэтому оставляем один корень |q2| ≈ 10-4 Кл.
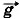 +
+ 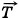 +
+ 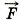 выт +
выт + 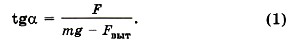
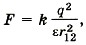 где r12 = 2l sinα, а выталкивающая сила
где r12 = 2l sinα, а выталкивающая сила