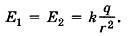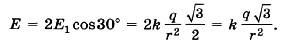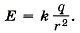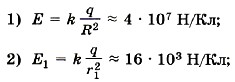|
|
|
|
|
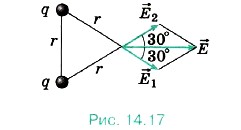
Глава 14. Электростатика § 91. Примеры решения задач по теме «Напряжённость электрического поля. Принцип суперпозиции полей»При решении задач с использованием понятия напряжённости электрического поля нужно прежде всего знать формулы (14.8) и (14.9), определяющие силу, действующую на заряд со стороны электрического поля, и напряжённость поля точечного заряда. Если поле создаётся несколькими зарядами, то для расчёта напряжённости в данной точке надо сделать рисунок и затем определить напряжённость как геометрическую сумму напряжённостей полей. Задача 1. Два одинаковых положительных точечных заряда расположены на расстоянии r друг от друга в вакууме. Определите напряжённость электрического поля в точке, расположенной на одинаковом расстоянии r от этих зарядов. Р е ш е н и е. Согласно принципу суперпозиции полей искомая напряжённость
Модули напряжённостей полей зарядов равны:
Диагональ параллелограмма, построенного на векторах
Задача 2. Проводящая сфера радиусом R = 0,2 м, несущая заряд q = 1,8 • 10-4 Кл, находится в вакууме. Определите: 1) модуль напряжённости Р е ш е н и е. Электрическое поле заряженной сферы вне её совпадает с полем точечного заряда. Поэтому Следовательно,
3) напряжённость поля в любой точке внутри проводящей сферы равна нулю: Е0 = 0.
|
|
|



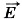 равна геометрической сумме напряжённостей полей, созданных каждым из зарядов (рис. 14.17):
равна геометрической сумме напряжённостей полей, созданных каждым из зарядов (рис. 14.17):