|
|
|
|
|
Глава 14. Электростатика Потенциальная энергия заряженного тела в однородном электростатическом полеЭлектрическое поле при перемещении заряда совершит положительную работу: А = qE(d1 - d2) = qEΔd. (14.12)
Докажем это непосредственным расчётом. Пусть перемещение заряда происходит по кривой (рис. 14.32). Разобьём эту кривую на малые перемещения. Сила, действующая на заряд, остаётся постоянной (поле однородно), а угол а между направлением силы и направлением перемещения будет изменяться. Работа на малом перемещении Δ
С помощью аналогичных рассуждений можно вывести формулу для работы кулоновской силы при перемещении заряда q0 из точки 1 в точку 2 в неоднородном поле неподвижного точечного заряда q. При этом должно быть учтено, что сила
Мы видим, что работа зависит только от положения начальной (r1) и конечной (r2) точек траектории и не зависит от формы траектории. Электростатическая сила, действующая на заряды, является так же, как и силы тяжести, тяготения и упругости, консервативной силой.
Потенциальная энергияПоскольку работа электростатической силы не зависит от формы траектории точки её приложения, сила является консервативной, и её работа согласно формуле (5.22) равна изменению потенциальной энергии, взятому с противоположным знаком: А = -(Wп2 - Wп1) = -ΔWп. (14.13) Сравнивая полученное выражение (14.12) с общим определением потенциальной энергии (14.13), видим, что ΔWп = Wп2 - Wп1 = -qEd. Считаем, что в точке 2 потенциальная энергия равна нулю. Тогда
|
|
|



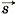 равна ΔА = qElΔ
равна ΔА = qElΔ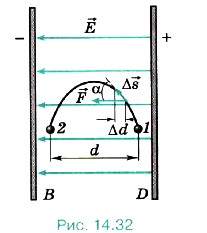
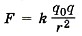 зависит от расстояния до точечного заряда q. Для работы кулоновской силы в поле точечного заряда q справедливо выражение
зависит от расстояния до точечного заряда q. Для работы кулоновской силы в поле точечного заряда q справедливо выражение
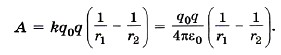
 Изобразите схематично однородное электрическое поле и начертите несколько траекторий, по которым движется заряд q. Покажите, что работа поля не зависит от траектории.
Изобразите схематично однородное электрическое поле и начертите несколько траекторий, по которым движется заряд q. Покажите, что работа поля не зависит от траектории.