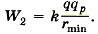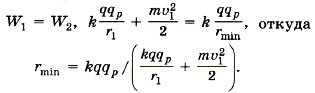|
|
|
|
|
Глава 14. Электростатика § 96. Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов»При решении задач надо учитывать, что работа сил, действующих на заряд со стороны поля, выражается через разность потенциальных энергий или разность потенциалов (см. формулу (14.20)). Потенциал однородного поля определяется формулой (14.16), при этом надо всегда указывать, как выбран нулевой уровень потенциала. Часто при решении задач надо учитывать, что все точки проводника в электростатическом поле имеют один и тот же потенциал, а напряжённость поля внутри проводника равна нулю. Задача 1. Определите значение напряжённости и потенциала поля в точке А, находящейся на расстоянии l = 20 см от поверхности заряженной проводящей сферы радиусом R = 10 см, если потенциал сферы φ0 = 240 В. Р е ш е н и е. Напряжённость поля сферы в точке А
где q0 — заряд сферы. Потенциал сферы и потенциал поля в точке А равны соответственно
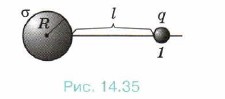
Выражая из формулы (2) заряд сферы q0 и подставляя полученное выражение в формулы (1) и (3), получаем для напряжённости Ел и потенциала Фл следующие выражения: ЕA = φ0R/(R + l)2 ≈ 267 Н/Кл, φA = φ0R/(R + l) = 80 В. Задача 2. Какую работу А необходимо совершить, чтобы перенести заряд q = 3 • 10-8 Кл из бесконечности в точку, находящуюся на расстоянии l = 90 см от поверхности сферы радиусом R = 10 см, если поверхностная плотность заряда сферы σ = 2 • 10-6 Кл/м2? Р е ш е н и е. Работа, совершаемая при перенесении заряда q из бесконечности в точку 1 (рис. 14.35), равна увеличению потенциальной энергии заряда:
A = ΔWп = Wп1 - W∞. Так как площадь поверхности сферы равна 4πR2, то заряд сферы равен 4πR2σ. Тогда потенциал поля в точке 1
Задача 3. К закреплённому заряженному шарику зарядом +q движется протон. На расстоянии r = r1 скорость протона υ1. Определите, на какое минимальное расстояние приблизится протон к шарику. Р е ш е н и е. Энергия протона на расстоянии r1 равна сумме его потенциальной и кинетической энергий: Кулоновская сила — консервативная, следовательно, можно записать закон сохранения энергии:
|
|
|





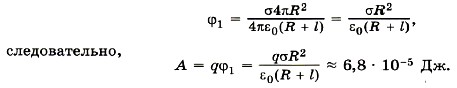
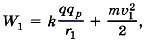 на расстоянии rmin (протон останавливается) — только потенциальной энергии:
на расстоянии rmin (протон останавливается) — только потенциальной энергии: