Главная >> Физика. 10 класс. Базовый уровень. Пурышева

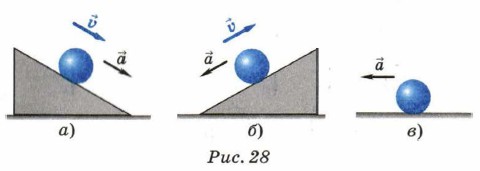
Глава 1. Механические явления

Основание классической механики

Галилей предположил, что шары падают равноускоренно, но этот факт невозможно было доказать на опыте, поскольку пришлось бы отмечать положения быстро падающих шаров через достаточно малые промежутки времени, а в XVI в. ещё не было точных приборов, позволяющих осуществлять подобные измерения. Поэтому Галилей исследовал качение шаров по наклонному деревянному жёлобу, тем самым замедлив их падение, и показал, что движение шаров равноускоренное. Формула для расчёта пути при равноускоренном движении без начальной скорости s = at²/2 была впервые получена именно Галилеем.

Анализируя результаты своих экспериментов, Галилей обосновал принцип инерции, прибегая для этого к следующим рассуждениям: опыты показывают, что, двигаясь по наклонной плоскости вниз, тело ускоряется (рис. 28, а), при движении вверх — замедляется (рис. 28, б). А если бесконечная плоскость не имеет наклона, то в таком случае нет причины, которая может заставить движущееся по ней тело ускориться или замедлиться (рис. 28, в). Таким образом,

в отсутствие внешнего воздействия тело находится в состоянии равномерного прямолинейного движения или покоя.

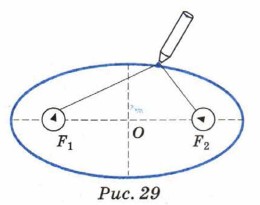
Галилей изучал акустику, колебания маятников, а в 1609 г. построил телескоп и наблюдал с его помощью Луну и планеты, открыл спутники Сатурна, увидел на Солнце пятна. Эти наблюдения, в частности, заставили Галилея окончательно принять гелиоцентрическую систему мира Коперника.

Астрономические наблюдения

2. Попытки проверить состоятельность системы мира Коперника с помощью астрономических наблюдений предпринимались не только Галилеем, но и другими учёными в XVI и начале XVII в. Так, датский астроном Тихо Браге (1546—1601) в течение многих лет проводил точные измерения положений и перемещений планет на небе. Результаты своего кропотливого труда он отразил в объёмных таблицах, которыми впоследствии воспользовался его ученик и последователь Кеплер. Дополнив данные Браге результатами собственных наблюдений, Кеплер эмпирически (из наблюдений) установил три закона, по которым происходит движение планет и других тел Солнечной системы.

Прежде чем сформулировать законы Кеплера, необходимо познакомиться с такой фигурой, как эллипс. На плоской доске закрепим концы нити (например, с помощью канцелярских кнопок) и, натягивая нить карандашом, начертим на доске замкнутую кривую (рис. 29). Мы получим эллипс.

Эллипсом называют геометрическое место точек, сумма расстояний от каждой из которых до двух данных точек — фокусов эллипса — одинакова. На рисунке обозначены: О — центр эллипса, F₁ и F₂ — его фокусы. Чем ближе друг к другу расположены фокусы эллипса, тем он ближе по форме к окружности. Если оба фокуса находятся в одной точке, то эллипс превращается в окружность. Первый закон Кеплера:

каждая из планет Солнечной системы движется по эллипсу, в одном из фокусов которого находится Солнце.

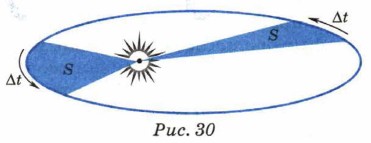
Второй закон Кеплера:

радиус, соединяющий центр Солнца с планетой, за равные промежутки времени описывает равные площади (рис. 30).

<<< К началу      Окончание >>>