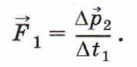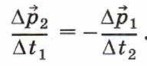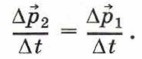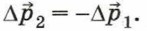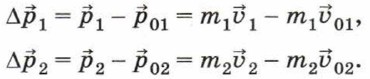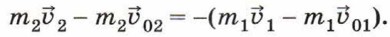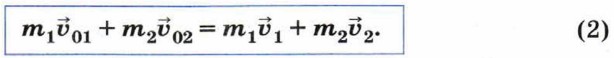|
|
|
|
|
Глава 2. Ядро классической механики Закон сохранения импульсаЗакон сохранения импульса2. Напомним, что при взаимодействии двух тел изменение импульса первого тела равно импульсу силы, действующей на него со стороны второго тела:
откуда
Аналогичное выражение можно записать для силы
Теперь необходимо учесть два обстоятельства. Во-первых, согласно третьему закону Ньютона,
Во-вторых, время действия тел друг на друга одно и то же, т. е. Δt1 = Δt2 = Δt, а значит,
Умножив обе части равенства на At, получим:
Перепишем это равенство, учитывая, что изменение импульса тела равно разности его импульсов после и до взаимодействия:
Тогда получим:
Теперь соберём импульсы тел, которыми они обладали до взаимодействия, в левой части равенства, а приобретённые после взаимодействия — в правой:
Импульс каждого из взаимодействующих тел изменился, однако векторная сумма их импульсов осталась неизменной. Рассмотренная система состояла из двух тел. Однако полученные выводы справедливы и в общем случае, когда система состоит из любого числа тел и является замкнутой: тела, составляющие такую систему, взаимодействуют между собой и не взаимодействуют с другими телами. Равенство (2) называют законом сохранения импульса.
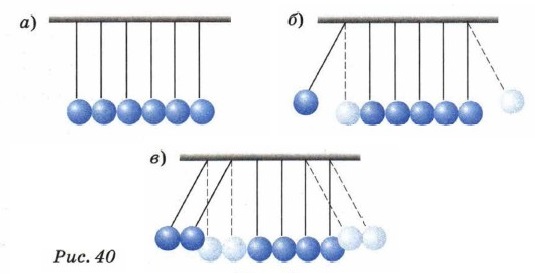
Проиллюстрировать закон сохранения импульса можно с помощью установки, состоящей из нескольких одинаковых шаров, подвешенных таким образом, что их центры лежат на одной прямой (рис. 40, а). Если отвести в сторону крайний левый шар и отпустить его, то он при ударе передаст свой импульс второму шару, второй — третьему и так далее. В результате можно наблюдать, что отскочит только один шар — тот, что висит с противоположной стороны цепочки шаров, а все остальные шары останутся на месте (рис. 40, б). Таким образом, импульс, потерянный при ударе первым шаром, был передан последнему шару, суммарный же импульс системы не изменился. Аналогичным образом можно отклонить в сторону и отпустить не один, а несколько шаров. Тогда после удара с противоположной стороны в движение придёт столько же шаров (рис. 40, в).
Закон сохранения импульса — это фундаментальный закон природы.
|
|
|



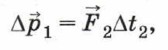
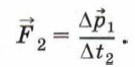
 1:
1: