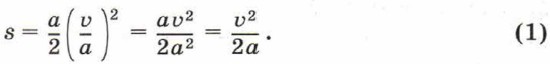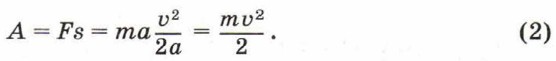|
|
|
|
|
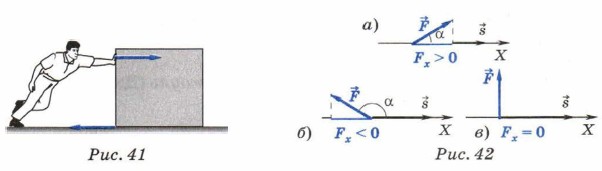
Глава 2. Ядро классической механики § 15. Закон сохранения механической энергииМеханическая работа1. Вам предстоит познакомиться с одной из теорем динамики, для чего необходимо вспомнить такие величины, как механическая работа и механическая энергия. О совершении механической работы можно говорить в том случае, когда тело перемещается под действием некоторой силы. Причём сила не обязательно должна способствовать перемещению тела: она может препятствовать его перемещению. Например, передвигая тумбу с одного места на другое, человек совершает над ней работу. Во время движения пол действует на тумбу, но трение о пол препятствует движению. Поскольку действие одного тела на другое характеризуется силой, то чаще всего говорят о механической работе, совершаемой какой-либо силой. Так, в рассмотренном примере над тумбой совершают работу две силы: одна из них действует со стороны человека, другая — со стороны пола (рис. 41).
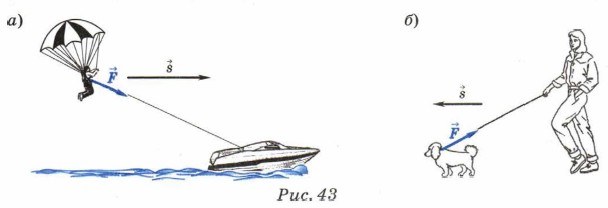
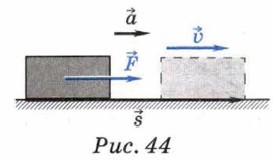
Если векторы силы и перемещения составляют острый угол (рис. 42, а), то работа положительна, поскольку значение косинуса острого угла положительно. Такую ситуацию можно наблюдать, например, при буксировке катером парапланера (рис. 43, а). В этом случае сила способствует движению тела. Если векторы силы и перемещения образуют тупой угол (рис. 42, б), то работа отрицательна: сила препятствует движению тела. Так, например, собаковод пытается помешать излишне резвому питомцу слишком быстро бежать (рис. 43, б). Работа не совершается силой, перпендикулярной перемещению (рис. 42, в): косинус прямого угла равен нулю, а значит, равна нулю и работа. Наибольшее по модулю значение механической работы получается в тех случаях, когда сила сонап- равлена перемещению (α = 0°, cos 0° = 1) или противонаправлена ему (α = 180°, cos 180° = -1).
Единица механической работы в СИ — джоуль (Дж). 1 Дж = 1 Н • м. Работа в 1 Дж совершается силой 1 Н при перемещении тела на 1 м. Механическая энергия2. Рассмотрим ситуацию, когда на покоящееся тело действует некоторая сила (рис. 44). Скорость, которую приобретёт тело через время t, и перемещение, совершённое за это время, можно рассчитать по известным вам формулам: υ = at и s = at2/2.
Выразим из формулы скорости время t = υ/a и подставим это выражение в формулу перемещения. Получим
Воспользовавшись выражением (1) и вторым законом Ньютона, вычислим работу силы по разгону тела до скорости υ:
В результате работы, совершённой силой при разгоне тела, оно приобрело некоторую скорость, и теперь само может совершить работу. Так, например, движущийся товарный вагон может, столкнувшись с другим вагоном, привести его в движение. О теле, которое способно совершить механическую работу, говорят, что оно обладает механической энергией. Таким образом, величину, стоящую в правой части выражения (2), называют механической энергией.
|
|
|



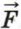 и перемещения
и перемещения 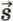 и косинуса угла α между этими векторами.
и косинуса угла α между этими векторами.