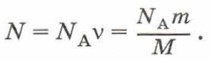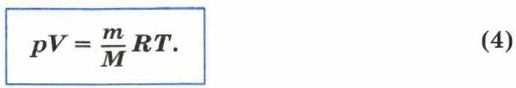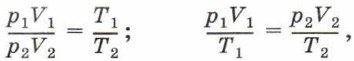Главная >> Физика. 10 класс. Базовый уровень. Пурышева

Глава 6. Свойства газов

Уравнение состояния идеального газа

Уравнение Менделеева—Клапейрона

3. Число молекул равно произведению постоянной Авогадро N_A на количество вещества ν, которое, в свою очередь, равно отношению массы газа m к его молярной массе М, т. е.:

Подставив это выражение в формулу (2), получим:

Произведение постоянной Больцмана k на постоянную Авогадро N_A называют универсальной газовой постоянной и обозначают буквой R.

R = kN_A = 8,31 Дж(моль • К).

Универсальная газовая постоянная показывает, какую энергию необходимо сообщить 1 моль идеального газа, чтобы увеличить его температуру на 1 К.

Заменив произведение kN_A на R в уравнении (3), запишем:

Уравнение (4) так же, как и уравнение (2), является уравнением состояния идеального газа; оно связывает параметры какого- либо состояния газа произвольной массы. Это уравнение называют уравнением Менделеева—Клапейрона.

Уравнение Клапейрона

4. Предположим, что газ переходит из некоторого состояния 1, которое характеризуется параметрами р₁, V₁, T₂, в состояние 2, которое характеризуется параметрами р₂, V₂, Т₂. При этом масса газа и его химический состав остаются неизменными. Запишем уравнение Менделеева—Клапейрона для первого и для второго состояний газа:

Разделим первое уравнение на второе. Получим:

или

Уравнение (5) называют уравнением Клапейрона. Это уравнение связывает параметры двух состояний газа при неизменной массе газа и его химическом составе.

Произведение давления газа данной массы и его объёма, делённое на термодинамическую температуру, есть величина постоянная.

<<< К началу      Окончание >>>