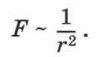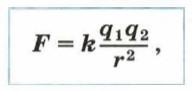|
|
|
|
|
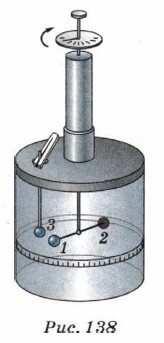
Глава 8. Электростатика § 48. Закон КулонаОпыты Кулона с крутильными весами1. Французский учёный Кулон в 1785 г. установил на опыте закон взаимодействия неподвижных электрических зарядов. Для выявления зависимости силы взаимодействия электрических зарядов от их модуля и расстояния между ними Кулон использовал специальный прибор — крутильные весы (рис. 138).
Крутильные весы представляют собой стеклянный цилиндр, внутри которого на тонкой серебряной нити подвешено лёгкое стеклянное коромысло. На одном конце коромысла закрепляется маленький металлический шарик 1, а на другом — противовес 2. Шарик 1 можно заряжать с помощью ещё одного металлического шарика 3, насаженного на стержень и закреплённого на крышке весов неподвижно. При соприкосновении шарика 1 и заряженного шарика 3 заряд распределяется между ними и шарики отталкиваются. По углу закручивания нити, который отсчитывается по шкале, можно определить силу взаимодействия зарядов. Проведя большое число опытов, Кулон установил, что сила взаимодействия двух заряженных шариков обратно пропорциональна квадрату расстояния между ними:
Заряд шарика 3 можно менять. При соприкосновении заряженного шарика с точно таким же незаряженным заряды распределятся поровну между шариками. В результате заряд на шарике 3 уменьшится в 2, 4, 8 и т. д. раз. Соответственно уменьшится и заряд шарика 1. Меняя заряды шариков, Кулон выяснил, что сила их взаимодействия прямо пропорциональна произведению зарядов: F ~ q1q2. Закон Кулона2. В результате обобщения данных многочисленных экспериментов Кулон сформулировал закон.
где q1 и q2 — модули зарядов, r — расстояние между точечными зарядами, k — коэффициент пропорциональности, зависящий от выбора единиц физических величин.
|
|
|