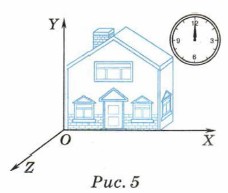
§ 5. Основные понятия классической механики

Макроскопические тела

1. Объекты, которые доступны наблюдению человеком даже без применения специальных приборов, называют макроскопическими. В настоящее время диапазон объектов, имеющих макроскопические размеры, увеличился: к их числу относят даже невидимые человеку тела, движение которых подчиняется законам классической механики. Условно считают, что нижней границей макромира являются тела, размеры которых не меньше 10-8 м. Таким образом, макроскопическими телами можно считать как космические объекты — звёзды, планеты и др., так и тела, окружающие человека на Земле, — деревья, камни, животных, а также песчинки, пылинки и т. д.

Пространство и время

2. Наблюдая за движением различных тел — падением камня со скалы, полётом стрелы, выпущенной из лука, парением птицы, бегом животного, течением реки, — люди стали рассуждать о таких категориях, как пространство и время. Эти понятия, несмотря на кажущуюся их простоту, относятся к числу сложнейших философских категорий. В классической механике, согласно пониманию Ньютона, принято считать, что пространство — «пустое вместилище» тел — однородно и изотропно (т. е. его свойства одинаковы во всех точках и по всем направлениям), а время однородно: оно равномерно течёт в одном направлении — от прошлого к будущему.

Тело отсчёта и система отсчёта

3. Из определения механического движения следует, что говорить о движении или покое тела можно лишь только относительно какого-либо другого тела — тела отсчёта. Для описания движения тела, т. е. определения его положения в пространстве, необходимо с телом отсчёта связать систему координат. Чаще всего используют декартову систему координат, в которой положение точки в пространстве задаётся тремя (на плоскости — двумя) координатами.

Поскольку движение происходит во времени, то при описании движения необходимо использовать прибор для измерения времени (часы). Таким образом,

тело отсчёта, связанная с ним система координат и часы составляют систему отсчёта (рис. 5).

часы составляют систему отсчёта

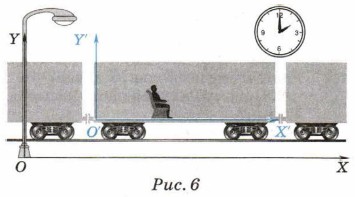
В зависимости от выбора той или иной системы отсчёта (тела отсчёта) рассматриваемое тело в одно и то же время может покоиться или двигаться. По этой причине говорят об относительности механического движения. Например, пассажир может покоиться относительно системы отсчёта Х'О'Y, связанной с вагоном поезда, в котором он едет (рис. 6), и в то же время вместе с поездом двигаться относительно системы отсчёта XOY, связанной с землёй.

время может покоиться или двигаться

Окончание >>>