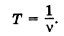|
|
|
|
|
Глава 1. Кинематика точки и твёрдого тела § 16. Кинематика абсолютно твёрдого телаПри любом ли движении тела можно использовать такую его модель, как материальная точка? Какие модели тела ещё существуют? Поступательное движение твёрдого тела. Описание движения тела считается полным лишь тогда, когда известно, как движется каждая его точка. Мы много внимания уделили описанию движения точки. Именно для точки вводятся понятия координат, скорости, ускорения, траектории. В общем случае задача описания движения тел является сложной. Особенно она сложна, если тела заметно деформируются в процессе движения. Проще описать движение тела, взаимное расположение частей которого не изменяется.
Абсолютно твёрдое тело — это одна из механических моделей, используемых при описании движения и взаимодействия тел. На самом деле абсолютно твёрдых тел нет. Но в тех случаях, когда реальные тела при движении мало деформируются, их можно рассматривать как абсолютно твёрдые. Однако и движение абсолютно твёрдого тела в общем случае оказывается весьма сложным. Самое простое движение абсолютно твёрдых тел — поступательное.
При поступательном движении все точки тела совершают одинаковые перемещения, описывают одинаковые траектории, проходят одинаковые пути, имеют в каждый момент времени равные скорости и ускорения. Покажем это.
Пусть тело движется поступательно (рис. 1.58). Соединим две его произвольные точки В и А отрезком. Расстояние |АВ| не изменяется, так как тело абсолютно твёрдое. При поступательном движении остаются постоянными модуль и направление вектора Согласно рисунку 1.58 перемещения точек А и В одинаковы и совершаются за одно и то же время. Очевидно, что любая точка твёрдого тела, например С, движется так же, как точки А и В. Следовательно, точки А и В имеют одинаковые скорости и ускорения. Совершенно очевидно, что для описания поступательного движения абсолютно твёрдого тела достаточно описать движение какой-либо одной его точки.
Примерно поступательно движутся ящик письменного стола, поршни двигателя автомобиля относительно цилиндров, вагоны на прямолинейном участке железной дороги, резец токарного станка относительно станины. Движение педали велосипеда или кабины колеса обозрения в парках (рис. 1.59, 1.60) — также примеры поступательного движения.
Вращательное движение абсолютно твёрдого тела. Вращательное движение вокруг неподвижной оси — ещё один частный случай движения твёрдого тела. В технике такой вид движения встречается очень часто: например, вращение валов двигателей и генераторов, турбин и пропеллеров самолётов.
Угловая скорость. Каждая точка тела, вращающегося вокруг неподвижной оси, проходящей через точку О, движется по окружности, и различные точки проходят за время Δt разные пути. Так, АА1 > ВВ1 (рис. 1.62), поэтому модуль скорости точки А больше, чем модуль скорости точки В. Но радиус-векторы, определяющие положение точек А и В, поворачиваются за время Δt на один и тот же угол Δφ. Угол φ — угол между осью ОХ и радиус-вектором Пусть тело вращается равномерно, т. е. за любые равные промежутки времени радиус-векторы поворачиваются на одинаковые углы. Чем больше угол поворота радиус-вектора, определяющего положение какой-то точки твёрдого тела, за определённый промежуток времени, тем быстрее вращается тело и тем больше его угловая скорость.
Будем обозначать угловую скорость греческой буквой ω (омега). Тогда по определению
Угловая скорость в СИ выражается в радианах в секунду (рад/с). Например, угловая скорость вращения Земли вокруг оси 0,0000727 рад/с, а точильного диска — около 140 рад/с. Угловую скорость можно связать с частотой вращения.
Если тело совершает ν (греческая буква «ню») оборотов за 1 с, то время одного оборота равно 1/ν секунд.
Таким образом, связь между частотой и периодом вращения можно представить в виде
|
|
|



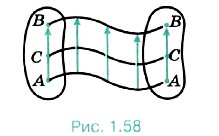
 . Вследствие этого траектории точек В и А одинаковы, так как они могут быть полностью совмещены параллельным переносом на вектор
. Вследствие этого траектории точек В и А одинаковы, так как они могут быть полностью совмещены параллельным переносом на вектор 
 В каком случае движение ручки, которой вы пишете, можно считать поступательным?
В каком случае движение ручки, которой вы пишете, можно считать поступательным?
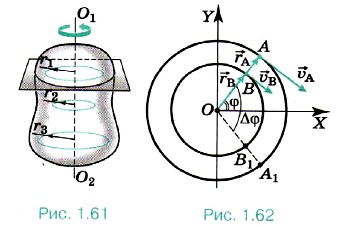
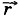 определяющим положение точки А (см. рис. 1.62).
определяющим положение точки А (см. рис. 1.62).