|
|
|
|
|
Глава 1. Кинематика точки и твёрдого тела § 17. Примеры решения задач по теме «Кинематика твёрдого телаПри решении задач по этой теме обращайте внимание на связь кинематических характеристик поступательного и вращательного движений. При этом могут быть в одних случаях одинаковыми угловые скорости (например, задача 2), а в других — линейные скорости движения (например, задача 1). Задача 1. Два шкива соединены ременной передачей, передающей вращение от одного шкива к другому. Ведущий шкив вращается с частотой ν1 = 3000 об/мин, ведомый шкив — с частотой ν2 = 600 об/мин. Ведомый шкив имеет диаметр D2 = 500 мм. Какой диаметр D1 у ведущего шкива? Р е ш е н и е. Ведущий шкив вращается с угловой скоростью ω1 = 2πν1, а ведомый — со скоростью ω2 = 2πν2. Скорость приводного ремня равна линейной скорости точек окружностей того и другого шкива: υ = ω1R1 = ω2R2. Отсюда
Задача 2. Колесо, радиус которого 40 см, катится по горизонтальной дороге со скоростью 2 м/с. Определите скорости относительно дороги точек колеса, находящихся на концах его вертикального и горизонтального диаметров, а также ускорения этих точек. Р е ш е н и е. Точка О1 неподвижна относительно земли (рис. 1.64), следовательно, υ1 = 0. Если считать, что через точку О1 проходит мгновенная ось вращения, то относительно неё скорости всех точек, согласно уравнению (1.29), будут равны υ = ωr, где r — расстояние от точки O1 до выбранной точки обода. Угловая скорость вращения ω = υ0/R. Тогда υc = υD = ωR√2 = υ0√2 ≈ 2,8 м/с. Скорость точки A υA = 2ωR = 2υ0 = 4 м/с. Все точки обода относительно оси вращения движутся с одинаковыми линейными скоростями и, следовательно, с одинаковым ускорениями
Заметим, что эту задачу также можно решить на основе закона сложения скоростей. Так, например, скорость точки D равна сумме скорости
Задача 3. Катушка с намотанной на неё нитью может катиться по поверхности горизонтального стола без скольжения. С какой скоростью υ0 и в каком направлении будет перемещаться ось катушки, если конец нити тянуть в горизонтальном направлении со скоростью υ? Радиус внутренней части катушки r, внешней — R (рис. 1.65).
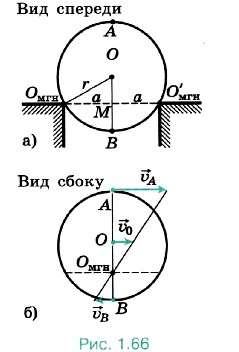
Р е ш е н и е. Скорость υ — скорость движения нити — совпадает со скоростью точки А внутренней части катушки. Омгн — мгновенная ось вращения. Угловая скорость относительно мгновенной оси вращения ω = υ/(R - r), так как расстояние ОмгнА = R - r. Отсюда υ0 = ωR = υR/(R - r). Очевидно, что катушка перемещается в направлении движения конца нити. Скорость перемещения катушки будет больше, чем скорость нити. Задача 4. Шарик радиусом r катится со скоростью υ0 по двум рельсам, расположенным на расстоянии 2а друг от друга. Определите скорости точек А и В относительно рельсов (рис. 1.66, а). Р е ш е н и е. Мгновенная ось вращения Омгн в данном случае показана на рисунке 1.66, б. Угловая скорость поворота шарика относительно этой оси ω = υ0/OM, где Отсюда следовательно, Задачи для самостоятельного решения1. Линейная скорость периферийных точек шлифовального камня не должна превышать 95 м/с. Определите наибольшее допустимое число оборотов в минуту для диска диаметром 30 см. 2. Длина минутной стрелки часов на Спасской башне Московского Кремля 3,5 м. Определите модуль и изменение направления линейной скорости конца стрелки через каждые 15 мин в течение часа. Повторите материал главы 1 по следующему плану 1. Выпишите основные понятия и физические величины и дайте им определение. 2. Сформулируйте законы и запишите основные формулы. 3. Укажите единицы физических величин и их выражение через основные единицы СИ. 4. Опишите основные опыты, подтверждающие справедливость законов.
1. Баллистическое движение. 2. Поступательное и вращательное движения в авиации. 3. Различные виды движения в производстве.
|
|
|



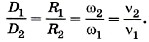 Следовательно, искомый диаметр
Следовательно, искомый диаметр 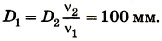
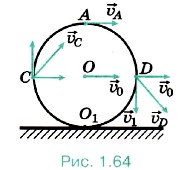
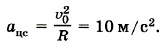
 0 подвижной системы отсчёта, связанной с осью колеса, и скорости
0 подвижной системы отсчёта, связанной с осью колеса, и скорости 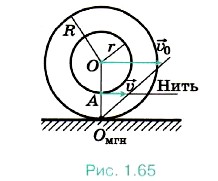
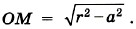
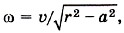
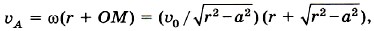
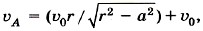
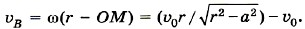
 «Движение во времени и в пространстве»
«Движение во времени и в пространстве»