|
|
|
|
|
Глава 1. Кинематика точки и твёрдого тела § 2. Способы описания движенияВспомните из курса физики основной школы физические величины, которыми можно описать механическое движение тела.
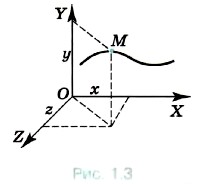
Если тело можно считать точкой, то для описания его движения нужно научиться рассчитывать положение точки в любой момент времени относительно выбранного тела отсчёта. Существует несколько способов описания, или, что одно и то же, задания движения точки. Рассмотрим два из них, которые наиболее часто применяются. Координатный способ. Будем задавать положение точки с помощью координат (рис. 1.3). Если точка движется, то её координаты изменяются с течением времени. Так как координаты точки зависят от времени, то можно сказать, что они являются функциями времени. Математически это принято записывать в виде
Если уравнения движения известны, то для каждого момента времени мы сможем рассчитать координаты точки, а следовательно, и её положение относительно выбранного тела отсчёта. Вид уравнений (1.1) для каждого конкретного движения будет вполне определённым.
Количество выбираемых для описания движения координат зависит от условий задачи. Если движение точки происходит вдоль прямой, то достаточно одной координаты и, следовательно, одного уравнения, например, x(t). Если движение происходит на плоскости, то его можно описать двумя уравнениями — x(t) и y(t). Уравнения (1.1) описывают движение точки в пространстве. Векторный способ. Положение точки можно задать, и с помощью радиус-вектора.
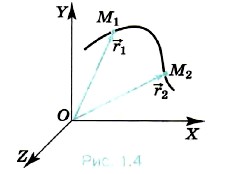
При движении материальной точки радиус-вектор, определяющий её положение, с течением времени изменяется (поворачивается и меняет длину; рис. 1.4), т. е. является функцией времени:
На рисунке 1.4 радиус-вектор
Если оно известно, то мы можем для любого момента времени рассчитать радиус-вектор точки, а значит, определить её положение.
Итак, мы знаем, что положение точки в пространстве определяется её координатами или её радиус-вектором. Модуль и направление любого вектора находят по его проекциям на оси координат. Чтобы понять, как это делается, вначале необходимо ответить на вопрос: что понимают под проекцией вектора на ось? Изобразим какую-либо ось (рис. 1.5), например ось ОХ. Опустим из начала А и конца В вектора
Проекцию вектора мы будем обозначать той же буквой, что и вектор, но, во-первых, без стрелки над ней и, во-вторых, с индексом внизу, указывающим, на какую ось проецируется вектор. Так, ах и ау — проекции вектора Согласно определению проекции вектора на ось можно записать: ах = ± |А1В1|.
Проекция вектора на ось представляет собой алгебраическую величину. Она выражается в тех же единицах, что и модуль вектора. Условимся считать проекцию вектора на ось положительной, если от проекции начала вектора к проекции его конца надо идти в положительном направлении оси проекций (рис. 1.6). В противном случае (см. рис. 1.5) она считается отрицательной. Из рисунков 1.5 и 1.6 нетрудно увидеть, что проекция вектора на ось будет положительной, когда вектор составляет острый угол φ с направлением оси проекций, и отрицательной, когда вектор составляет с направлением оси проекции тупой угол φ.
Вопросы к параграфу 1. Какими способами можно задать положение точки? 2. Как задают положение точки в пространстве с помощью координат? 3. Что называется радиус-вектором? 4. Что называется проекцией вектора на ось? 5. Чему равна проекция вектора на ось, если вектор направлен так же, как и ось проекции? 6. Чему равна проекция вектора на ось, если вектор направлен противоположно оси проекции? 7. Чему равна проекция вектора на перпендикулярную к нему ось?
|
|
|




 Сколько координат необходимо для описания движения: машины по прямой дороге; бильярдного шара по столу; мухи по комнате?
Сколько координат необходимо для описания движения: машины по прямой дороге; бильярдного шара по столу; мухи по комнате?
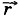 =
= 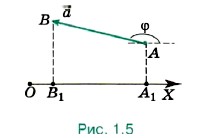
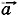 перпендикуляры на ось ОХ. Точки А1 и В1 есть проекции соответственно начала и конца вектора
перпендикуляры на ось ОХ. Точки А1 и В1 есть проекции соответственно начала и конца вектора 
 Иногда нужно находить составляющие вектора, например векторы
Иногда нужно находить составляющие вектора, например векторы