|
|
|
|
|
Глава 1. Кинематика точки и твёрдого тела
§ 20. Первый закон НьютонаКакое явление называют инерцией? Что называют системой отсчёта? Закон инерции относится к самому простому случаю движения — движению тела, которое не взаимодействует с другими телами, т. е. движению свободного тела. Ответить на вопрос, как же движутся свободные тела, не обращаясь к опыту, нельзя. Однако нельзя поставить ни одного опыта, который бы в чистом виде показал, как движется ни с чем не взаимодействующее тело, так как таких тел нет. Как же быть? Имеется лишь один выход. Надо поместить тело в условия, при которых влияние внешних взаимодействий можно делать всё меньшим и меньшим, и наблюдать, к чему это ведёт. Можно, например, наблюдать за движением гладкого камня на горизонтальной поверхности, после того как ему сообщена некоторая скорость. (Притяжение камня к Земле компенсируется действием поверхности, на которую он опирается; на скорость его движения влияет только трение.) При этом легко обнаружить, что, чем более гладкой является поверхность, тем медленнее будет уменьшаться скорость камня. На гладком льду камень скользит весьма долго, не меняя заметно скорость. На основе подобных наблюдений можно сделать вывод: если бы поверхность была идеально гладкой, то при отсутствии сопротивления воздуха (в вакууме) камень совсем не менял бы своей скорости. Именно к такому выводу пришёл впервые Галилей. Сформулируем первый закон Ньютона:
Этот закон, с одной стороны, содержит определение инерциальной системы отсчёта. С другой стороны, он содержит утверждение (которое с той или иной степенью точности можно проверить на опыте) о том, что инерциальные системы отсчёта существуют в действительности. Инерциальные и неинерциальные системы отсчёта. До сих пор систему отсчёта мы связывали с Землёй, т. е. рассматривали движение относительно Земли. В системе отсчёта, связанной с Землёй, ускорение тела определяется только действием на него других тел. Система отсчёта, связанная с Землёй, является инерциальной. Из формулировки первого закона следует, что
Однако, помимо инерциальных систем отсчёта, есть и другие, в которых тело имеет ускорение даже в том случае, когда на него другие тела не действуют. В качестве примера рассмотрим систему отсчёта, связанную с автобусом. При равномерном движении автобуса пассажир может не держаться за поручень, действие со стороны автобуса компенсируется взаимодействием с Землёй. При резком торможении автобуса стоящие в проходе пассажиры падают вперёд, получая ускорение относительно стенок автобуса (рис. 2.6). Однако это ускорение не вызвано какими-либо новыми воздействиями со стороны Земли или автобуса непосредственно на пассажиров. Относительно Земли пассажиры сохраняют свою постоянную скорость, но автобус начинает двигаться с ускорением, и пассажиры относительно него также движутся с ускорением. Ускорение появляется вследствие того, что движение их рассматривается относительно тела отсчёта (автобуса), движущегося с ускорением.
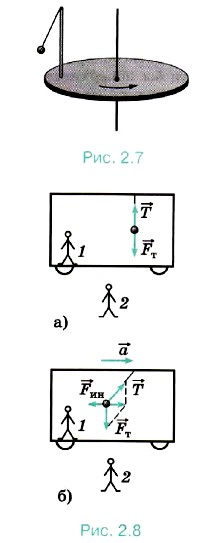
Рассмотрим маятник, находящийся на вращающемся диске (рис. 2.7). Нить маятника отклонена от вертикали, хотя сам он неподвижен относительно диска. Натяжение нити не может быть скомпенсировано силой притяжения к Земле. Следовательно, отклонение маятника нельзя объяснить только его взаимодействием с телами. Рассмотрим ещё один маятник, находящийся в неподвижном вагоне. Нить маятника вертикальна (рис. 2.8, а). Шарик взаимодействует с нитью и Землёй, сила натяжения нити равна силе тяжести. С точки зрения пассажира в вагоне и человека, стоящего на перроне, шарик находится в равновесии вследствие того, что сумма сил, действующих на него, равна нулю. Как только вагон начинает двигаться с ускорением, нить маятника отклоняется (шарик по инерции стремится сохранить состояние покоя). С точки зрения человека, стоящего на перроне, ускорение шарика должно быть равно ускорению вагона, так как нить не разрывается и шарик движется вместе с вагоном. Шарик по-прежнему взаимодействует с теми же телами, сумма сил этого взаимодействия должна быть отлична от нуля и определять ускорение шарика. С точки зрения пассажира, находящегося в вагоне, шарик неподвижен, следовательно, сумма сил, действующих на шарик, должна быть равна нулю, однако на шарик действуют те же силы — натяжения нити и сила Рис. 2.8 тяжести. Значит, на шарик (рис. 2.8, б) должна действовать сила В неинерциальных системах отсчёта основное положение механики о том, что ускорение тела вызывается действием на него других тел, не выполняется.
Вопросы к параграфу 1. Какое утверждение содержится в первом законе Ньютона? 2. Какая система отсчёта называется инерциальной? 3. Каким образом можно установить, что данная система отсчёта является инерциальной? 4. Если за инерциальную систему отсчёта принять Землю, то какие надо выбрать на Земле тела отсчёта, чтобы системы, связанные с ними, были также инерциальными?
|
Первыи закон, или закон инерции, как его часто называют, фактически был открыт Галилеем, но строгую формулировку дал и включил его в число основных законов механики Исаак Ньютон.
Приведите примеры инерциальных и неинерциальных систем отсчёта.
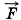ин, которая определяется тем, что система отсчёта, связанная с вагоном, неинерциальная. Эту силу называют силой инерции (см. рис. 2.8, б).
|
|