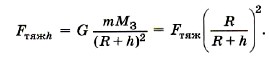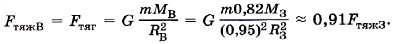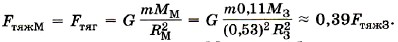|
|
|
|
|
Глава 3. Силы в механике § 29. Сила тяжести на других планетаЧем различаются сила тяжести и сила тяготения? Что влияет на значение силы тяжести? Сила тяжести возникает в результате взаимодействия тела с Землёй при учёте суточного вращения Земли.
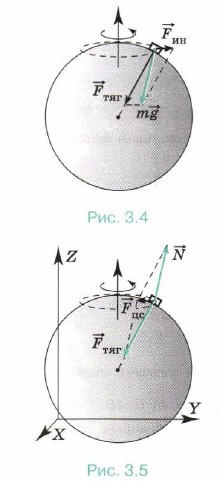
Поясним, как влияет суточное вращение Земли на значение силы тяжести. Как мы знаем, Земля вращается вокруг собственной оси с периодом, равным 24 часам. Следовательно, система отсчёта, связанная с Землёй, является неинерциальной, и тело, находящееся на Земле, находится в неинерциальной системе отсчёта (рис. 3.4). Вследствие этого на тело действует, помимо силы тяготения, центробежная сила инерции, равная гто2г и направленная от центра окружности, по которой вращается тело. Равнодействующая этих двух сил и будет силой тяжести, равной Ускорение свободного падения не направлено по радиусу к центру Земли, а направлено, как мы видим, под углом к этому радиусу. Центростремительное ускорение зависит от радиуса окружности, по которой движется тело, следовательно, сила тяжести и ускорение свободного падения зависят от широты местности. На полюсе ускорение свободного падения максимально и равно 9,83 м/с2, а на экваторе минимально и равно 9,78 м/с2. Рассмотрим движение тела относительно инерциальной системы отсчёта, например системы, связанной со звёздами (рис. 3.5). Запишем согласно второму закону Ньютона уравнение движения тела m
Так как согласно закону всемирного тяготения
На Луне и других планетах сила тяжести отличается от силы тяжести на Земле, так как изменяется сила тяготения. Сила тяготения, как мы видели, определяется массой планеты и её радиусом. Масса и радиус Луны меньше, чем масса и радиус Земли, поэтому сила тяжести на Луне существенно меньше. Так, на тело массой 1 кг на Луне действует сила тяжести, равная 1,7 Н. Рассчитаем силу тяжести, действующую на тело массой 1 кг, находящееся на поверхности Венеры, при этом пренебрежём влиянием вращения Венеры вокруг собственной оси. Это можно сделать потому, что период вращения Венеры вокруг собственной оси почти в 10 раз больше, чем аналогичный период вращения Земли. Масса Венеры МB = 0,82М3, радиус RB = 0,95 R3. Тогда
Соответственно и ускорение свободного падения на Венере равно gB = 0,91g3 ≈ 8,9 м/с2. Таким образом, ускорение свободного падения на Венере несущественно отличается от ускорения свободно падения на Земле. Если рассматривать другие планеты, например Марс, то сила тяжести на Марсе уже существенно отличается от силы тяжести, действующей на то же тело на Земле. Радиус Марса равен 0,53 радиуса Земли, а масса — 0,11 Следовательно, Таким образом, ускорение свободного падения на Марсе приблизительно равно 3,8 м/с2.
Вопросы к параграфу 1. Где на планете, вращающейся относительно собственной оси, сила тяжести максимальна? 2. Как определить силу тяжести на планете, зная массу планеты и массу тела? 3. Космонавт, находясь на Земле, притягивается к ней с силой 700 Н. С какой силой он будет притягиваться к Марсу, находясь на его поверхности, если радиус Марса примерно в 2 раза, а масса в 10 раз меньше, чем у Земли? 4. Планета имеет радиус, в 2 раза меньший радиуса Земли. Известно, что ускорение свободного падения на поверхности этой планеты такое же, как на Земле. Чему равно отношение массы этой планеты к массе Земли?
|
|
|



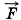 тяж = m
тяж = m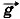 =
= 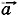 цc.
цc.
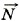 , где
, где  Что влияет на силу тяжести, действующую на тела, находящиеся на Луне? Обсудите эту проблему с одноклассниками.
Что влияет на силу тяжести, действующую на тела, находящиеся на Луне? Обсудите эту проблему с одноклассниками.
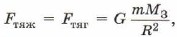 то после преобразований можно получить, что сила тяжести, действующая на тело, находящееся на расстоянии h над поверхностью Земли, равна
то после преобразований можно получить, что сила тяжести, действующая на тело, находящееся на расстоянии h над поверхностью Земли, равна