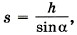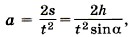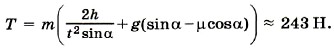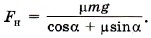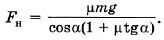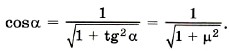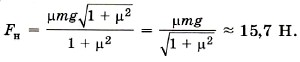|
|
|
|
|
Глава 3. Силы в механике § 37. Примеры решения задач по теме «Силы трения»При решении задач о движении тел, на которые действует сила трения, надо всегда иметь в виду, что сила трения скольжения, действующая на тело, направлена в сторону, противоположную относительной скорости движения. Поэтому, чтобы нарисовать вектор силы трения, прежде всего надо определить направление движения тела.
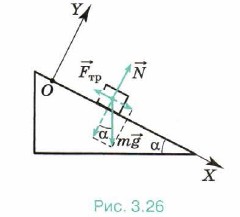
Задача 1. В результате полученного толчка кирпич начал скользить вниз по неподвижной ленте конвейера, расположенной под углом α = 30° к горизонтальной плоскости. Определите модуль и направление ускорения кирпича, если коэффициент трения скольжения кирпича о ленту конвейера μ = 0,6. Р е ш е н и е. Направим ось ОХ вдоль наклонной ленты конвейера вниз, а ось OY перпендикулярно ленте конвейера вверх (рис. 3.26). Так как кирпич движется вдоль оси ОХ, то его ускорение может быть направлено только вдоль этой оси вниз либо вверх. По второму закону Ньютона m Запишем уравнение (1) в проекциях на оси ОХ и OY: mаx = mg sinα - Fтр, (2)
Модуль силы трения скольжения выразим через коэффициент трения р и модуль силы нормальной реакции опоры N: Fтр = μN = μmg cosα. (3) Подставив выражение (3) в уравнение (2), получим mах = mg sin&alpha - μm cosα. Окончательно а = g(sin&alpha - μcosα).
Из формулы следует, что проекция ускорения кирпича на ось ОХ может быть положительной, отрицательной и равной нулю: если sina > μcosα, то ах > 0 (вектор ускорения направлен вдоль ленты конвейера вниз); если sinα = μcosα, то ах = 0 (кирпич движется без ускорения); наконец, если sinα < μcosα, то ах < 0 (вектор ускорения направлен вдоль ленты конвейера вверх). Для случая, рассматриваемого в задаче, ах = -0,2 м/с2. Следовательно, ускорение кирпича направлено вдоль ленты конвейера вверх и модуль этого ускорения а = 0,2 м/с2. Задача 2. В кузове автомобиля лежит ящик массой 30 кг. Определите, с каким максимальным ускорением может двигаться автомобиль, начинающий движение, чтобы ящик не сдвинулся. Коэффициент трения ящика о пол кузова равен μ = 0,3. Р е ш е н и е. Автомобиль движется с ускорением. Чтобы ящик оставался неподвижным, необходимо, чтобы ускорение ящика было равно ускорению автомобиля.
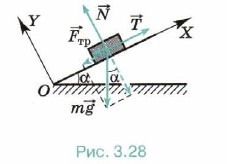
В начале движения автомобиля ящик должен двигаться в сторону, противоположную движению автомобиля, так как по инерции стремится сохранить состояние покоя. Автомобиль движется вправо (рис. 3.27). Тогда скорость ящика относительно автомобиля должна быть направлена влево, следовательно, сила трения должна быть направлена вправо. На ящик действуют сила тяжести m m В проекциях на горизонтальное и вертикальное направления запишем: mа = Так как по условию задачи мы должны найти максимальное ускорение, то в пределе сила трения покоя должна быть равна силе трения скольжения: Подставим это выражение в уравнение (2) и получим mа = μN. Из уравнения (3) следует, что N = mg. Тогда mа = μxmg и а = μg ≈ 3 м/с2. Задача 3. По наклонной плоскости тянут равноускоренно за канат ящик массой 50 кг. Угол у основания наклонной плоскости 30°, коэффициент трения 0,2. Ящик поднимают на высоту 20 м за 5 с. Определите силу натяжения каната.
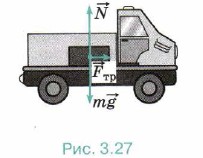
Р е ш е н и е. На ящик действуют сила тяжести m Согласно второму закону Ньютона m В проекциях на оси ОХ и OY уравнение имеет вид mа = Т - mg sinα - Сила трения скольжения Из уравнения (3) получим N = mg cosa. Уравнение (2) перепишем в виде mа = Т - mg sinα - μmg cosα. Ускорение определим из уравнения движения
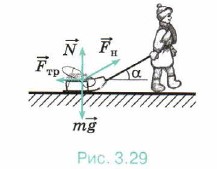
Задача 4. Девочка тянет равномерно по снегу нагруженные санки массой 40 кг. Коэффициент трения санок о снег 0,04. Определите, под каким углом должна быть расположена верёвка, чтобы её натяжение было минимально.
Р е ш е н и е. На санки действуют сила натяжения верёвки m Так как движение по условию равномерное, то ускорение а = 0. Запишем уравнение (1) в проекциях на горизонтальное и вертикальное направления: 0 = Fн cosα - Fтp; (2)
Из уравнения (3) получим N = mg - Fн sinα. Подставив в уравнение (2) выражение для силы трения Fтp = μx(mg - Fн sinα), получим Fн cosα - μx(mg - Fн sinα) = 0. Для силы натяжения имеем Сила натяжения минимальна при максимальном значении суммы cosα + μsinα = ƒ(α). Исследуем функцию на экстремум: ƒ' = -sinα + μcosα = 0. Получим tgα = μ. Тогда Выразим cosa через tgα: Окончательно для силы натяжения получим
|
|
|



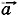 = m
= m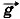 +
+ 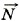 +
+ 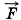 тр. (1)
тр. (1)
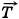 . (1)
. (1)
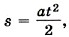 при этом
при этом