|
|
|
|
|
Глава 4. Закон сохранения импульса § 39. Примеры решения задач по теме «Закон сохранения импульса»Закон сохранения импульса целесообразно применять для решения тех задач, в которых требуется определить скорость, а не силу или ускорение. Для решения задачи нужно записать этот закон в векторной форме: m1 После этого векторное уравнение записывается в проекциях на оси выбранной системы координат. Выбор направления осей диктуется удобством решения задачи. Если, например, все тела движутся вдоль одной прямой, то координатную ось целесообразно направить вдоль этой прямой. При решении некоторых задач приходится использовать дополнительно уравнения кинематики. Задача 1. Два шара, массы которых m1 = 0,5 кг и m2 = 0,2 кг, движутся по гладкой горизонтальной поверхности навстречу друг другу со скоростями υ1 = 1 м/с и υ2 = 4 м/с. Определите их скорость v после центрального абсолютно неупругого столкновения.
Р е ш е н и е. Ось ОХ направим вдоль линии, проходящей через центры движущихся шаров по направлению скорости После абсолютно неупрутого удара шары движутся с одной и той же скоростью m1υ1x + m2υ2x = (m1 + m2)υx. Так как υ1x = υ1, a υ2x = -υ2, то υx = (m1υ1 - m2υ2)/(m1 + m2) ≈ -0,4 м/с. После удара шары будут двигаться в отрицательном направлении оси ОХ со скоростью 0,4 м/с.
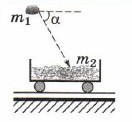
Задача 2. Два пластилиновых шарика, отношение масс которых m2/m1 = 4, после соударения слиплись и стали двигаться по гладкой горизонтальной поверхности со скоростью и (рис. 4.3, вид сверху). Определите скорость более лёгкого шарика до соударения, если он двигался в 3 раза быстрее тяжёлого (υ1 = 3υ2), а направления движения шариков были взаимно перпендикулярны. Трением можно пренебречь. Р е ш е н и е. Так как скорости Согласно закону сохранения импульса имеем m1 Запишем это уравнение в проекциях на оси ОХ и OY, проведённые так, как показано на рисунке 4.3: m1υ1x + m2υ2x = (m1 + m2)их,
Так как υ1x = υ1, υ2x = 0, υ1y = 0, υ2y = υ2y = υ2, то
Модуль скорости и равен Итак, υ2 = и, следовательно, υ1 = 3и. Можно эту задачу решить так. Импульсы Тогда Задача 3. Компоненты топлива в двигатель ракеты подаются со скоростью υ1 = 200 м/с, а горючий газ выходит из сопла со скоростью υ2 = 500 м/с. Массовый расход топлива двигателем Р е ш е н и е. Изменение импульса топлива массой Δm за время Δt равно Δmυ2 - Δmυ1 = FΔt. Тогда сила, подействовавшая на горючий газ, вырывающийся из сопла ракеты,
Согласно третьему закону Ньютона сила, подействовавшая на топливо, равна по модулю и противоположна по направлению силе, подействовавшей на ракету, т. е. реактивной силе
Задачи для самостоятельного решения1. Неподвижный вагон массой 2 • 104 кг сцепляется с платформой массой 3 • 104 кг. До сцепки платформа имела скорость 1 м/с. Чему равна скорость вагона и платформы после их сцепки? 2. На плот массой 100 кг, имеющий скорость 1 м/с, направленную вдоль берега, прыгает человек массой 50 кг со скоростью 1,5 м/с перпендикулярно берегу. Определите скорость плота с прыгнувшим на него человеком. 3. Будет ли увеличиваться скорость ракеты, если скорость истечения газов относительно ракеты меньше скорости самой ракеты и вытекающие из сопла газы летят вслед за ракетой? 4. Охотник стреляет с лёгкой надувной лодки. Определите скорость лодки после выстрела, если масса охотника 70 кг, масса дроби 35 г и средняя начальная скорость дробинок равна 320 м/с. Ствол ружья во время выстрела образует с горизонтом угол 60°.
Повторите материал главы 4 по следующему плану1. Выпишите основные понятия и физические величины и дайте им определение. 2. Сформулируйте законы и запишите основные формулы. 3. Укажите единицы физических величин и их выражение через основные единицы СИ. 4. Опишите основные опыты, подтверждающие справедливость законов.
|
|
|



 1 + m2
1 + m2 1 + m2
1 + m2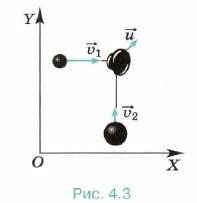
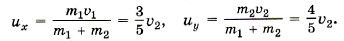
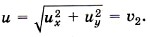
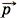 1 и
1 и 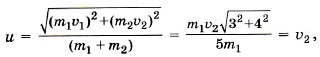 и, следовательно, υ1 = 3и.
и, следовательно, υ1 = 3и.
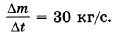 Определите реактивную силу.
Определите реактивную силу.
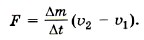
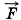 = -
= -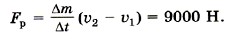
 «Ракетные двигатели и использование реактивного движения для полётов в безвоздушном пространстве»
«Ракетные двигатели и использование реактивного движения для полётов в безвоздушном пространстве»
 «Э. К. Циолковский. Идеи Циолковского (по его работам) и их реальное воплощение»
«Э. К. Циолковский. Идеи Циолковского (по его работам) и их реальное воплощение»