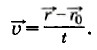|
|
|
|
|
Глава 1. Кинематика точки и твёрдого тела § 4. Равномерное прямолинейное движение. Скорость. Уравнение движенияОдин и тот же путь тело может пройти за разные промежутки времени. Какая физическая величина характеризует быстроту движений тела? Как, зная эту величину, определить положение тела? На уроках физики вы довольно подробно изучали равномерное движение.
Равномерное движение может быть как криволинейным, так и прямолинейным. Равномерное прямолинейное движение — самый простой вид движения. С него мы и начнём изучение движения в кинематике. Скорость. Важной величиной, характеризующей движение точки, является её скорость. Некоторое представление о скорости каждый из нас имел и до начала изучения физики. Черепаха перемещается с малой скоростью, человек движется с большей скоростью, автомобиль движется быстрее человека, а самолёт — ещё быстрее. Самой большой скорости относительно Земли человек достигает с помощью космических ракет.
В механике рассматривают скорость как векторную величину. А это означает, что скорость можно считать известной (заданной) лишь в том случае, если известны её модуль и направление.
Дадим определение скорости равномерного прямолинейного движения точки. Пусть точка, двигаясь равномерно и прямолинейно в течение промежутка времени Δt, переходит из положения М1 в положение М2 (рис. 1.9), совершив при этом перемещение Δ (При делении вектора на число получаем вектор.) Этот вектор называют скоростью равномерного прямолинейного движения точки и обозначают буквой
Так как промежуток времени Δt — величина положительная, то скорость направлена так же, как и перемещение Δ
Модуль перемещения |Δ Уравнение равномерного прямолинейного движения точки. Пусть радиус-вектор
Если начальный момент времени t0 принять равным нулю, то
Отсюда
Последнее уравнение и есть уравнение равномерного прямолинейного движения точки, записанное в векторной форме. Оно позволяет найти радиус-вектор точки при этом движении в любой момент времени, если известны скорость точки и радиус-вектор, задающий её положение в начальный момент времени. Вместо векторного уравнения (1.4) можно записать три эквивалентных ему уравнения в проекциях на оси координат. Радиус-вектор
|
|
|



 Составьте с помощью Интернета таблицу примерных скоростей различных объектов. Проанализируйте её.
Составьте с помощью Интернета таблицу примерных скоростей различных объектов. Проанализируйте её.
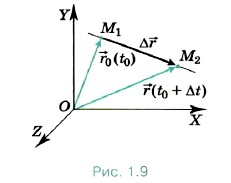
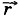 . Поделим перемещение Δ
. Поделим перемещение Δ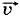 . Следовательно, можно записать:
. Следовательно, можно записать:

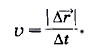
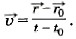
 Проведите эксперимент. Измерьте время вашего перемещения из одной точки в другую, например от двери школы до калитки. Определите скорость. Сравните вашу скорость со скоростью товарища, прошедшего это же расстояние.
Проведите эксперимент. Измерьте время вашего перемещения из одной точки в другую, например от двери школы до калитки. Определите скорость. Сравните вашу скорость со скоростью товарища, прошедшего это же расстояние.