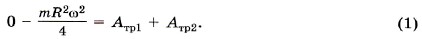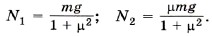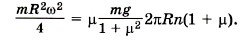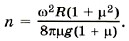|
|
|
|
|
Глава 6. Динамика вращательного движения абсолютно твёрдого тела § 50. Примеры решения задач по теме «Динамика вращательного движения абсолютно твёрдого тела»При решении задач на эту тему следует иметь в виду, что моменты силы, инерции и импульса зависят от выбора оси вращения. Кроме этого, нужно обращать внимание на то, что моменты импульса всех тел записываются относительно одной и той же системы отсчёта.
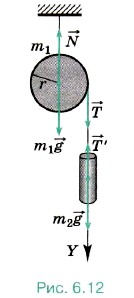
Задача 1. На блок радиусом r и массой m1 намотана нить, к концу которой привязан груз массой m2 (рис. 6.12). Груз отпускают, и он движется вниз, раскручивая нить. Определите ускорение груза. Массой нити можно пренебречь. Р е ш е н и е. Обозначим на рисунке силы, действующие на блок и груз. На блок действуют сила тяжести m1 На груз действуют сила тяжести m2 Согласно второму закону Ньютона в проекции на ось Y для груза запишем: m2a = m2g - T'. (1) Согласно основному закону динамики вращательного движения для блока запишем: Iε = Tr. (2) Момент инерции блока Так как по условию задачи нить невесома, то Т = Т'. Преобразуем уравнение (2): Подставив это выражение в уравнение (1), получим Окончательно Задача 2. Скамья Жуковского радиусом 1 м со стоящим в центре человеком вращается, делая 2 об/с. Человек переходит на край скамьи. Определите изменение угловой скорости вращения скамьи. Масса человека 50 кг, момент инерции скамьи 30 кг • м2. Р е ш е н и е. Так как внешние силы — сила тяжести и сила реакции опоры, направленные параллельно оси вращения, не могут изменить момент импульса системы тел «скамья—человек», то согласно закону сохранения импульса I1ω1 = I2ω2. (1) Когда человек находится в центре скамьи, то момент инерции системы равен только моменту инерции скамьи: I1 = Iск. После того как человек перешёл на край скамьи, момент инерции системы стал равен I2 = Iск + mr2. Угловая скорость связана с числом оборотов в секунду соотношением ω1 = 2πn. Подставив найденные выражения в уравнение (1), получим Iск2πn = (Iск + mr2)ω2. Тогда Изменение угловой скорости Задача 3. На наклонную плоскость вкатывается колесо, двигавшееся по горизонтальной поверхности со скоростью 4 м/с. Вся масса колеса сосредоточена в ободе. Определите максимальную высоту, на которую поднимется колесо. Работой силы трения можно пренебречь.
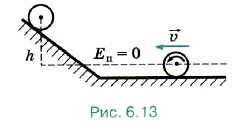
Р е ш е н и е. Выберем нулевой уровень отсчёта потенциальной энергии так, как показано на рисунке 6.13. Учтём, что момент инерции колеса-обруча I = mR2, а угловая скорость вращения ω = υ/R. Механическая энергия колеса на горизонтальной поверхности равна сумме кинетических энергий поступательного и вращательного движений колеса:
На максимальной высоте механическая энергия равна потенциальной энергии Е2 = mgh. Согласно закону сохранения механической энергии получим Е1 = Е2, или mυ2 = mgh, откуда h = υ2/g = 1,6 м. Задача 4. Сплошной цилиндр раскрутили до угловой скорости ω и положили на пол к стенке. Коэффициент трения между стенкой, полом и цилиндром μ, радиус цилиндра R. Определите, сколько оборотов сделает цилиндр до остановки.
Р е ш е н и е. Решаем задачу, используя теорему об изменении кинетической энергии. При этом учтём, что ось вращения цилиндра неподвижна, момент инерции цилиндра относительно этой оси равен Изменение кинетической энергии равно алгебраической сумме работ сил, действующих на него:
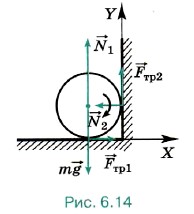
На цилиндр (рис. 6.14) действуют силы тяжести m Так как перемещается относительно стенок угла только точка приложения сил трения, то работу совершают только силы трения. В связи с этим справедливо уравнение
Работы сил трения равны Aтp1 = -Fтp12πRn; Aтp2 = -Fтp12πRn, где n — число полных оборотов цилиндра до остановки, а силы трения определяются силами реакции опоры стенок на цилиндр: Fтp1 = μN1; Fтp2 = μN2. Найдём силы реакции опоры. По условию задачи цилиндр только вращается, его центр тяжести не движется, следовательно, векторная сумма сил, действующих на него, равна нулю: m В проекциях на оси ОХ и OY имеем Fтp1 - N2 = 0; (2)
Подставив в уравнения (2) и (3) выражения для сил трения, получим μN1 - N2 = 0; (4)
Решая систему уравнений (4) и (5), найдём силы реакции опоры:
Тогда число оборотов до остановки цилиндра
Задачи для самостоятельного решения
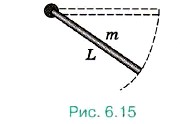
1. На блок радиусом 10 см и массой 1 кг по касательной действует сила 6 Н. Определите, через какой промежуток времени скорость блока станет равной 5 рад/с. 2. На шарнире в горизонтальном положении удерживают однородный стержень длиной 60 см и массой 1 кг (рис. 6.15). Стержень отпускают, и он начинает вращение. Определите максимальную линейную скорость стержня в тот момент, когда он проходит положение равновесия. Какая точка стержня будет двигаться с этой скоростью? Момент инерции стержня I = mL2/3. Повторите материал главы б по следующему плану1. Выпишите основные понятия и физические величины и дайте им определение. 2. Сформулируйте законы и запишите основные формулы. 3. Укажите единицы физических величин, характеризующих вращательное движение твёрдого тела, и их выражение через основные единицы СИ. 4. Опишите основные опыты, подтверждающие справедливость законов.
|
|
|



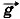 , сила реакции
, сила реакции 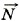 опоры и сила натяжения
опоры и сила натяжения 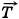 нити.
нити.
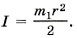 Связь углового и линейного ускорений а = εr.
Связь углового и линейного ускорений а = εr.
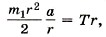 тогда
тогда 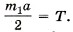
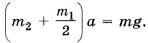
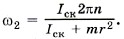
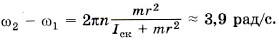
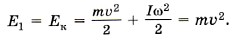
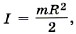 соответственно кинетическая энергия цилиндра вначале равна
соответственно кинетическая энергия цилиндра вначале равна 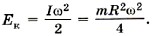
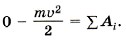
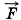 тр1,
тр1,