|
|
|
|
|
Глава 9. Молекулярно-кинетическая теория идеального газа § 58. Примеры решения задач по теме «Основное уравнение молекулярно-кинетической теории»Обратим внимание на то, что в задачах, как правило, имеется в виду средняя квадратичная скорость поступательного движения молекул. Связь этой скорости с макропараметрами, такими, как давление и температура, и устанавливает основное уравнение молекулярно-кинетической теории. Именно поступательное движение молекул определяет их удары о стенку и силу, действующую на неё. Задача 1. Плотность газа в баллоне электрической лампы ρ = 0,9 кг/м2. При горении лампы давление в ней возросло с р1 = 8 • 104 Па до р2 = 1,1 • 105 Па. На сколько увеличилось при этом значение среднего квадрата скорости молекул газа? Р е ш е н и е. Произведение массы т0 одной молекулы на концентрацию молекул (число молекул в единице объёма) равно массе молекул, заключённых в единице объёма, т. е. плотности газа р = т0п. Следовательно, основное уравнение молекулярно-кинетической теории (9.6) можно записать в виде Поэтому Задача 2. Определите плотность кислорода ρO при давлении 2 • 105 Па, если средний квадрат скорости его молекул равен 106 (м/с)2. Р е ш е н и е. Давление кислорода Окончательно имеем Задача 3. Два одинаковых сосуда, содержащие одинаковое число молекул азота, соединены краном. В первом сосуде средний квадрат скорости молекул Р е ш е н и е. Разные скорости молекул в сосудах объясняются разными температурами азота в них. Так как по условию задачи число молекул, имеющих скорость υ1, равно числу молекул, имеющих скорость υ2 (N1 = N2), то квадрат средней скорости
Задача 4. С какой скоростью растёт толщина покрытия стенки серебром при напылении, если атомы серебра, обладая энергией Р е ш е н и е. Если за время Δt толщина слоя серебра стала равной Δl, то скорость роста толщины покрытия есть Δl/Δt. Объём напылённого слоя ΔV = SΔl, где S - площадь поверхности стенки. Этот объём можно выразить иначе:
где m — масса серебряного покрытия, напылённого за время Δt, m0 — масса атома, N — число атомов. Определим суммарную массу атомов серебра, осевших на стенку. Изменение импульса атома, осевшего на стенку со скоростью υ, равно импульсу силы, подействовавшей на стенку со стороны атома: ƒτ = m0Δυ = m0(0 - υ) = -m0υ. На стенку подействует импульс силы ƒстτ = +m0υ. Если на стенку за время Δt осядет N атомов, то импульс силы, подействовавший на стенку в результате ударов о неё N атомов, будет FΔt = Nυm0. Давление на стенку р = F/S, или р = Nυm0/SΔt. (1) Средняя кинетическая энергия атома Подставив выражение для скорости в формулу (1), получим
тогда
Масса атома серебра m0 = A/NA, где NA = 6,02 • 1023 моль-1. Подставив это выражение в формулу (2), получим
Задачи для самостоятельного решения 1. Температура воздуха в комнате изменилась от 7 до 27 °С. На сколько процентов уменьшилось число молекул в комнате? 2. Под каким давлением находится газ в сосуде, если средний квадрат скорости его молекул 3. В колбе объёмом 1,2 л содержится 3 • 1022 атомов гелия. Чему равна средняя кинетическая энергия каждого атома? Давление газа в колбе 105 Па. 4. Вычислите средний квадрат скорости движения молекул газа, если его масса m = 6 кг, объём V = 4,9 м3 и давление р = 200 кПа.
|
|
|



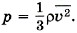
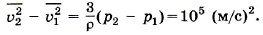
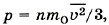 где n — концентрация молекул. Очевидно, что ρ = mOn, где mO — масса молекулы кислорода.
где n — концентрация молекул. Очевидно, что ρ = mOn, где mO — масса молекулы кислорода.
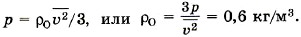
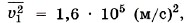 во втором сосуде —
во втором сосуде — 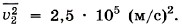 Кран открывают. Чему будет равен средний квадрат скорости молекул после того, как установится равновесие?
Кран открывают. Чему будет равен средний квадрат скорости молекул после того, как установится равновесие?
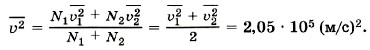
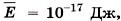 , производят на стенку давление р = 0,1 Па? Атомная масса серебра А = 1,108 г/моль, его плотность ρ = 10,5 г/см3.
, производят на стенку давление р = 0,1 Па? Атомная масса серебра А = 1,108 г/моль, его плотность ρ = 10,5 г/см3.
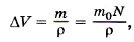
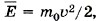 отсюда скорость атома
отсюда скорость атома 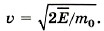
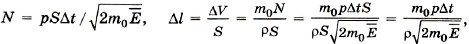

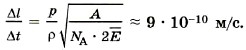
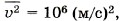 концентрация молекул n = 3 • 1025 м-3, масса каждой молекулы m0 = 5 • 10-26 кг?
концентрация молекул n = 3 • 1025 м-3, масса каждой молекулы m0 = 5 • 10-26 кг?