|
|
|
|
|
Глава 13. Основы термодинамики
§ 81. Второй закон термодинамикиВспомните формулировку первого закона термодинамики. Допускает ли первый закон термодинамики самопроизвольный переход тепла от менее нагретого тела к более нагретому? Наблюдаются ли такие процессы в природе? Мы уже отмечали, что первый закон термодинамики — это частный случай закона сохранения энергии. Закон сохранения энергии утверждает, что количество энергии при любых её превращениях остаётся неизменным. Между тем многие процессы, вполне допустимые с точки зрения закона сохранения энергии, никогда не протекают в действительности. Например, с точки зрения первого закона термодинамики в изолированной системе возможен переход тепла от менее нагретого тела к более нагретому, если количество теплоты, полученной горячим телом, точно равно количеству теплоты, отданной холодным телом. В то же время наш опыт подсказывает, что это невозможно.
Второй закон термюдинамики. Второй закон термодинамики указывает направление возможных энергетических превращений, т. е. направление процессов, и тем самым выражает необратимость процессов в природе. Этот закон был установлен путём непосредственного обобщения опытных фактов. Есть несколько формулировок второго закона, которые, несмотря на внешнее различие, выражают, в сущности, одно и то же и поэтому равноценны. Немецкий учёный Р. Клаузиус (1822—1888) сформулировал этот закон так:
Здесь констатируется опытный факт определённой направленности теплопередачи: тепло само собой переходит всегда от горячих тел к холодным. Правда, в холодильных установках осуществляется теплопередача от холодного тела к более тёплому, но эта передача связана с другими изменениями в окружающих телах: охлаждение достигается за счёт работы. Важность этого закона в том, что из него можно вывести заключение о необратимости не только процесса теплопередачи, но и других процессов в природе.
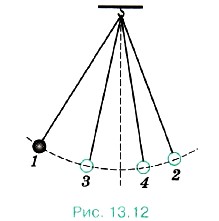
Рассмотрим пример. Колебания маятника, выведенного из положения равновесия, затухают (рис. 13.12) 1, 2, 3, 4 — последовательные положения маятника при максимальных отклонениях от положения равновесия). За счёт работы сил трения механическая энергия маятника убывает, а температура маятника и окружающего воздуха (а значит, и их внутренняя энергия) слегка повышается. Можно вновь увеличить размах колебаний маятника, подтолкнув его рукой. Но это увеличение возникает не само собой, а становится возможным в результате более сложного процесса, включающего движение руки.
Ещё один пример — процесс диффузии. Открыв пузырёк с духами, мы быстро почувствуем запах духов. Молекулы ароматического вещества благодаря тепловому движению проникают в пространство между молекулами воздуха. Трудно представить, чтобы все они вновь собрались в пузырьке. Число подобных примеров можно увеличивать практически неограниченно. Все они говорят о том, что процессы в природе имеют определённую направленность, никак не отражённую в первом законе термодинамики.
В обратном направлении они самопроизвольно протекать не могут. Все процессы в природе необратимы. Раньше при рассмотрении процессов мы предполагали, что они являются обратимыми.
Обратимый процесс должен протекать очень медленно, чтобы каждое промежуточное состояние было равновесным.
Следовательно, чтобы система пришла в равновесное состояние, необходимо время.
При изучении изопроцессов мы предполагали, что переход из начального состояния в конечное проходит через равновесные состояния, и считали изотермический, изобарный и изохорный процессы обратимыми. Идеальных обратимых процессов в природе не существует, однако реальные процессы можно с определённой степенью точности рассматривать как обратимые, что является очень важным для теории.
Статистический характер второго закона термодинамики. Второй закон термодинамики определяет направление процессов в изолированной системе, однако этот закон носит статистический (вероятностный) характер. Любое макросостояние системы, характеризующееся некоторыми макропараметрами, определяется его микросостояниями. Например, для газа давление и температура определяются числом молекул, их скоростью, распределением молекул по объёму сосуда. Если система предоставлена самой себе и она изолирована, то, как мы знаем, постепенно достигается равновесное состояние, при котором давление и температура во всех точках одинаковы. Процесс перехода системы из неравновесного состояния в равновесное — необратимый процесс. Равновесное состояние соответствует хаотичному движению молекул, т. е. система с точки зрения микросостояний приходит к полному хаосу. Хаотичное движение предполагает непрерывное перемещение молекул газа по объёму, обмен скоростями. Естественно, если мы сможем проследить за отдельными молекулами, то они в разные моменты времени оказываются в разных частях сосуда. Число молекул, находящихся в выделенном объёме, также может быть различным и т. д. В то же время макропараметры газа не меняются. Движение молекул — это механическое движение, которое является обратимым. В то же время все необратимые процессы, такие, как теплообмен, происходят вследствие механического движения атомов и молекул, так как столкновения молекул обеспечивают передачу энергии. Итак, необратимые процессы являются следствием обратимого механического движения. Чтобы соединить эти два неоспоримых факта, Л. Больцман использовал понятие вероятности. Так, состояние газа, при котором молекулы движутся хаотично, является наиболее вероятным, наиболее вероятным является и равномерное распределение молекул по объёму сосуда. Однако возможно, что благодаря случайным перемещениям молекул все они окажутся в какой-то части сосуда, но вероятность такого состояния чрезвычайно мала. Соответственно не противоречит законам природы даже такой процесс, в результате которого при случайном движении молекул воздуха все они соберутся в одной половине класса, а учащиеся в другой половине класса задохнутся. Но реально это событие никогда не происходило в прошлом и не произойдёт в будущем. Слишком мала вероятность подобного события, чтобы оно когда-либо случилось за всё время существования Вселенной в современном её состоянии — около нескольких миллиардов лет. По приблизительным оценкам, эта вероятность примерно такого же порядка, как и вероятность того, что 20 000 обезьян, хаотично ударяя по клавишам пишущих машинок, напечатают без единой ошибки «Войну и мир» Л. Н. Толстого. В принципе это возможно, но реально никогда не произойдёт. Границы применимости второго закона термодинамики. Вероятность обратных процессов перехода от равновесных состояний к неравновесным для макроскопических систем в целом очень мала. Но для малых объёмов, содержащих небольшое число молекул, вероятность отклонения от равновесия становится заметной.
Именно флуктуациями плотности газа в областях порядка длины световой волны объясняются рассеяние света в атмосфере Земли и голубой цвет неба. Флуктуации давления в малых объёмах объясняют броуновское движение. Наблюдение флуктуации служит важнейшим доказательством правильности созданной Больцманом статистической теории необратимости макропроцессов. Второй закон термодинамики выполняется только для систем с огромным числом частиц. В малых объёмах уже становятся существенными отклонения от этого закона.
Вопросы к параграфу 1. Какие процессы называются необратимыми? Назовите наиболее типичные необратимые процессы. 2. Как формулируется второй закон термодинамики? 3. Какое состояние газа является наиболее вероятным и соответствует равновесному состоянию?
|
Как вы понимаете термин «направление процесса»?
Яркой иллюстрацией необратимости явлений в природе служит просмотр кинофильма в обратном направлении. Например, прыжок в воду будет при этом выглядеть следующим образом. Спокойная вода в бассейне начинает бурлить, появляются ноги, стремительно движущиеся вверх, а затем и весь ныряльщик. Поверхность воды быстро успокаивается. Постепенно скорость ныряльщика уменьшается, и вот уже он спокойно стоит на вышке. Такой процесс, как вознесение ныряльщика на вышку из воды, не противоречит ни закону сохранения энергии, ни законам механики, ни вообще каким-либо законам, кроме второго закона термодинамики.
|
|