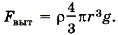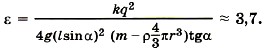|
|
|
|
|
Глава 14. Электростатика При решении задач на применение закона Кулона используются те же приёмы, что и при решении задач в курсе механики. Надо лишь иметь в виду, что направление кулоновской силы зависит от знаков зарядов взаимодействующих тел. Кроме того, в ряде задач используется закон сохранения заряда и тот факт, что заряд любого тела кратен заряду электрона. Задача 1. Сколько электронов содержится в капле воды массой m = 0,03 г? Масса молекулы воды m0 = 3 • 10-23 г. Р е ш е н и е. Молекула воды (Н2O) содержит 10 электронов. В капле воды содержится Задача 2. Два одинаковых шарика подвешены на нитях длиной I = 2,0 м к одной точке. Когда шарикам сообщили одинаковые заряды по q = 2,0 • 10-8 Кл, они разошлись на расстояние r = 16 см. Определите натяжение каждой нити и массу каждого шарика.
Р е ш е н и е. На каждый шарик действуют три силы: сила тяжести m Каждый шарик неподвижен, следовательно, суммы проекций сил на оси ОХ и OY равны нулю. Для суммы проекций сил, действующих на правый шарик, на ось ОХ это условие имеет вид F - Т sinα = 0. Так как
В проекциях на ось OY условие равновесия для каждого из шариков имеет вид Tcosα - mg = 0, откуда с учётом того, что cos2α = 1 — sin2α, получим
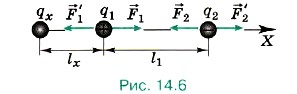
Задача 3. Два разноимённых заряда q1 = 2 • 10-4 Кл и q2 = -8 • 10-4 Кл расположены на расстоянии 1 м друг от друга. Какой заряд qx и где надо поместить, чтобы система зарядов находилась в равновесии?
Р е ш е н и е. Заряды q1 и q2 разноимённые, следовательно, они притягиваются и на них действуют силы
В проекциях на ось X эти уравнения имеют вид F1 = F'1, F2 = F'2, или
Решим полученную систему уравнений относительно двух неизвестных qx и lx. Из первого уравнения выразим |qx|: Получим уравнение Решением этого уравнения, удовлетворяющим физическому смыслу, является lx - 1 м. Подставив это значение в формулу для |qx|, получим |qx| = |q2| = 8 • 10-4 Кл, или qx = -8 • 10-4 Кл. Задача 4. Два заряженных шарика, находящиеся друг от друга на расстоянии r = 90 см и помещённые в керосин, притягиваются друг к другу с силой F = 80 Н. Определите заряды шариков, если сумма их зарядов q = 4 • 10-5 Кл. Относительная диэлектрическая проницаемость керосина ε = 2. Р е ш е н и е. Так как шарики притягиваются, то их заряды противоположны по знаку. Предположим, что заряд первого шарика положителен и равен q1, а второго отрицателен и равен q2. Согласно условию задачи q1 + q2 = q, или q1 - |q2| = q. (1) По закону Кулона сила притяжения зарядов равна:
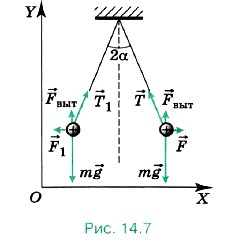
Уравнения (1) и (2) — система двух уравнений относительно двух неизвестных q1 и |q2|. Выразив из уравнения Относительно модуля заряда |q2| получим уравнение Отсюда Таким образом, q2 = -10-4 Кл, a q1 = 1,4 • 10-4 Кл. Задача 5. Два одинаковых небольших одноимённо заряженных шарика радиусом 1 см, массой 10 г и зарядом 4 • 10-6 Кл подвешены в одной точке на двух нитях длиной 1 м в жидком диэлектрике. Плотность диэлектрика ρ = 800 кг/м3. Определите относительную диэлектрическую проницаемость диэлектрика ε, если угол между нитями 2α = 60°.
Р е ш е н и е. На каждый шарик действуют сила тяжести, сила натяжения нити, выталкивающая сила и сила Кулона (рис. 14.7). Условия равновесия шариков m В проекциях на оси координат для правого шарика запишем: на ось OX: -Tsinα + F = 0; на ось ОY: -mg + Tcosα + Fвыт = 0. Выразив силу Т из этих уравнений и приравняв правые части полученных выражений, найдём
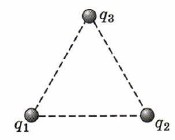
При этом сила Кулона Подставим эти выражения в уравнение (1) и найдём диэлектрическую проницаемость:
Задачи для самостоятельного решения 1. Определите силу взаимодействия электрона с ядром в атоме водорода, если расстояние между ними равно 0,5 • 10-8 см. 2. С какой силой взаимодействовали бы две капли воды на расстоянии 1 км, если бы удалось передать одной из капель 1% всех электронов, содержащихся в другой капле массой 0,03 г? 3. Два одинаковых шарика находятся на расстоянии 40 см друг от друга. Заряд одного из них 9 • 10-9 Кл, а заряд другого -2 • 10-9 Кл. Шарики привели в соприкосновение и вновь раздвинули на такое же расстояние. Определите силы их взаимодействия до и после соприкосновения. 4. Точечные заряды 1,0 • 10-8 Кл и 2,0 • 10-8 Кл закреплены на расстоянии 1 м друг от друга в вакууме. На середине отрезка, соединяющего эти заряды, на одинаковом расстоянии от каждого из них помещён точечный заряд, равный -3 • 10-9 Кл. Определите модуль и направление силы, действующей на него. 5. Два одинаковых маленьких шарика подвешены в одной точке на нитях длиной 1 м в масле с диэлектрической проницаемостью ε = 2,2. Шарикам сообщили одинаковые заряды 9 • 10-6 Кл, при этом нити разошлись на угол 60°. Определите массу каждого шарика. Размерами шариков можно пренебречь.
|
|
|



 молекул, и, следовательно, число электронов
молекул, и, следовательно, число электронов 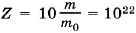 электронов.
электронов.
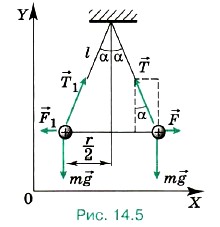
 сила натяжения нити и кулоновская сила (рис. 14.5).
сила натяжения нити и кулоновская сила (рис. 14.5).
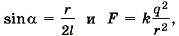 то
то
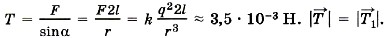
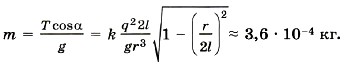
 1 и
1 и 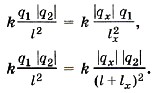
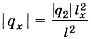 — и подставим во второе.
— и подставим во второе.
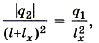 или
или 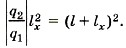 Подставим значения зарядов:
Подставим значения зарядов: 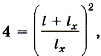 или
или 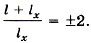

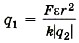 и подставив в уравнение (1), получим
и подставив в уравнение (1), получим 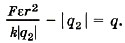
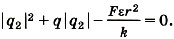
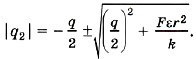 Модуль числа всегда положителен, поэтому оставляем один корень |q2| ≈ 10-4 Кл.
Модуль числа всегда положителен, поэтому оставляем один корень |q2| ≈ 10-4 Кл.
 +
+ 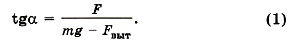
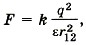 где r12 = 2l sinα, а выталкивающая сила
где r12 = 2l sinα, а выталкивающая сила