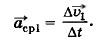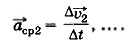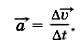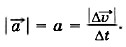|
|
|
|
|
Глава 1. Кинематика точки и твёрдого тела § 9. УскорениеКак изменяются показания спидометра в начале движения и при торможении автомобиля? Какая физическая величина характеризует изменение скорости?
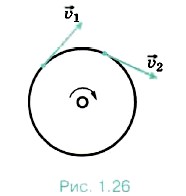
При движении тел их скорости обычно меняются либо по модулю, либо по направлению, либо жеодновременно как по модулю, так и по направлению. Скорость шайбы, скользящей по льду, уменьшается с течением времени до полной остановки. Если взять в руки камень и разжать пальцы, то при падении камня его скорость постепенно нарастает. Скорость любой точки окружности точильного круга при неизменном числе оборотов в единицу времени меняется только по направлению, оставаясь постоянной по модулю (рис 1.26). Если бросить камень под углом к горизонту, то его скорость будет меняться и по модулю, и по направлению. Изменение скорости тела может происходить как очень быстро (движение пули в канале ствола при выстреле из винтовки), так и сравнительно медленно (движение поезда при его отправлении).
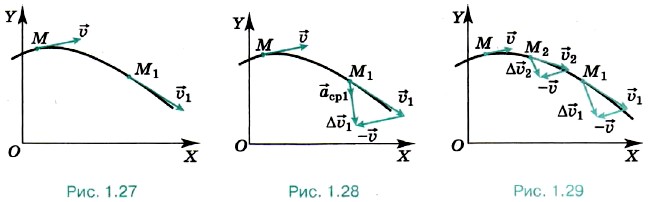
Рассмотрим случай криволинейного и неравномерного движения точки. В этом случае её скорость с течением времени изменяется как по модулю, так и по направлению. Пусть в некоторый момент времени t точка занимает положение М и имеет скорость Δ Согласно правилу сложения векторов вектор изменения скорости Δ
Поделив вектор Δ
По аналогии с определением мгновенной скорости определим мгновенное ускорение. Для этого найдём теперь средние ускорения точки за всё меньшие и меньшие промежутки времени:
При уменьшении промежутка времени Δt вектор Δ
Ускорение направлено так, как направлен вектор изменения скорости Δ
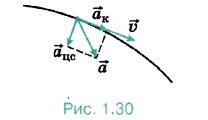
В общем случае ускорение направлено под углом к вектору скорости (рис. 1.30). Полное ускорение характеризует изменение скорости и по модулю, и по направлению. Часто полное ускорение Единица ускорения. Движение точки может происходить как с переменным, так и с постоянным ускорением. Если ускорение точки постоянно, то отношение изменения скорости к промежутку времени, за которое это изменение произошло, будет одним и тем же для любого интервала времени. Поэтому, обозначив через Δt некоторый произвольный промежуток времени, а через Δ
Так как промежуток времени Δt — величина положительная, то из этой формулы следует, что если ускорение точки с течением времени не изменяется, то оно направлено так же, как и вектор изменения скорости. Таким образом, если ускорение постоянно, то его можно истолковать как изменение скорости в единицу времени. Это позволяет установить единицы модуля ускорения и его проекций. Запишем выражение для модуля ускорения:
Отсюда следует, что
Если время измерено в секундах, а скорость — в метрах в секунду, то единица ускорения — м/с2 (метр на секунду в квадрате).
Вопросы к параграфу 1. Что называется ускорением? 2. Куда направлено ускорение при прямолинейном движении точки, если модуль скорости точки увеличивается? уменьшается? 3. Точка движется по криволинейной траектории с постоянной по модулю скоростью. Имеет ли эта точка ускорение? 4. Может ли точка иметь ускорение, если её скорость в данный момент времени равна нулю? 5. В каких единицах выражается ускорение? 6. Автомобиль движется по шоссе с постоянной скоростью и начинает тормозить. Как направлена проекция ускорения на ось, направленную по вектору начальной скорости автомобиля? 7. Как направлено ускорение равномерно движущейся по окружности точки? 8. Можно ли утверждать, что если ускорение точки постоянно, то направление её скорости не изменяется? 9. Лыжник съехал с горы, двигаясь прямолинейно и равноускоренно. За время 20 с, в течение которых длился спуск, скорость лыжника возросла от 5 м/с до 15 м/с. С каким ускорением двигался лыжник?
|
|
|



 Подбросьте вверх мяч и сделайте вывод об изменении его скорости.
Подбросьте вверх мяч и сделайте вывод об изменении его скорости.
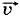 (рис. 1.27). Спустя промежуток времени Δt точка займёт положение М1 и будет иметь скорость
(рис. 1.27). Спустя промежуток времени Δt точка займёт положение М1 и будет иметь скорость  Приведите друг другу примеры движения тел, при которых изменения скорости происходят только по направлению или только по модулю.
Приведите друг другу примеры движения тел, при которых изменения скорости происходят только по направлению или только по модулю.
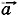 cр1, запишем:
cр1, запишем: