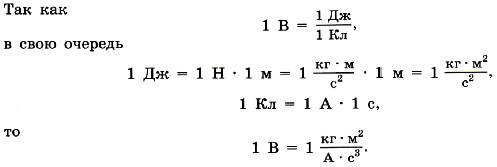|
|
|
|
|
Глава 14. Электростатика § 94. Потенциал электростатического поля и разность потенциаловОбладает ли электрическое поле энергией? В чём это выражается? Как рассчитать энергию поля? В механике взаимное действие тел друг на друга характеризуют силой и потенциальной энергией. Электростатическое поле, осуществляющее взаимодействие между зарядами, также характеризуют двумя величинами. Напряжённость поля — это силовая характеристика. Теперь введём энергетическую характеристику — потенциал. Потенциал поля. Работа любого электростатического поля при перемещении в нём заряженного тела из одной точки в другую также не зависит от формы траектории, как и работа однородного поля.
Потенциальный характер, в частности, имеет электростатическое поле точечного заряда. Работу потенциального поля можно выразить через изменение потенциальной энергии. Формула А = - (Wп2 - Wп1) справедлива для любого электростатического поля. Но только в случае однородного поля потенциальная энергия выражается формулой (14.14). Потенциальная энергия заряда в электростатическом поле пропорциональна заряду. Это справедливо как для однородного поля (см. формулу (14.14)), так и для неоднородного. Следовательно,
Это позволяет ввести новую количественную характеристику поля — потенциал, не зависящую от заряда, помещённого в поле. Для определения значения потенциальной энергии, как мы знаем, необходимо выбрать нулевой уровень её отсчёта. При определении потенциала поля, созданного системой зарядов, как правило, предполагается, что потенциал в бесконечно удалённой точке поля равен нулю.
Согласно данному определению потенциал равен:
Из этой формулы следует, что потенциал поля неподвижного точечного заряда q в данной точке поля, находящейся на расстоянии r от заряда, равен:
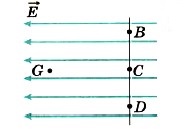
Напряжённость поля Если в примере с двумя заряженными пластинами в качестве точки с нулевым потенциалом выбрать точку на отрицательно заряженной пластине (см. рис. 14.31), то согласно формулам (14.14) и (14.15) потенциал однородного поля в точке, отстоящей на расстоянии d от неё, равен:
Разность потенциалов. Подобно потенциальной энергии, значение потенциала в данной точке зависит от выбора нулевого уровня для отсчёта потенциала, т. е. от выбора точки, потенциал которой принимается равным нулю.
Так как потенциальная энергия Wn = дчр, то работа сил поля равна: А = - (Wп2 - Wп1) = -q(φ2 - φ1) = q(φ1 - φ2) = qU. (14.17) Здесь U = φ1 - φ2 — (14.18) разность потенциалов, т. е. разность значений потенциала в начальной и конечной точках траектории.
Согласно формулам (14.17) и (14.18) разность потенциалов между двумя точками оказывается равной:
Если за нулевой уровень отсчёта потенциала принять потенциал бесконечно удалённой точки поля, то потенциал в данной точке равен отношению работы электростатических сил по перемещению положительного заряда из данной точки в бесконечность к этому заряду. Единица разности потенциалов. Единицу разности потенциалов устанавливают с помощью формулы (14.19). В Международной системе единиц работу выражают в джоулях, а заряд — в кулонах.
Выразим единицу разности потенциалов через основные единицы СИ. Так как
Вопросы к параграфу 1. Какие поля называют потенциальными? 2. Как разность потенциалов между двумя точками поля зависит от работы электрического поля? 3. Что нужно выбрать сначала, прежде чем говорить о значении потенциала в данной точке поля?
|
|
|



 Как называются силы, поле которых потенциально? Подумайте, почему они так называются.
Как называются силы, поле которых потенциально? Подумайте, почему они так называются.
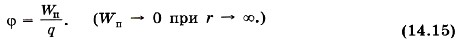
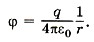
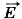 — векторная величина. Она представляет собой силовую характеристику поля, которая определяет силу, действующую на заряд q в данной точке поля. А потенциал φ — скаляр, это энергетическая характеристика поля; он определяет потенциальную энергию заряда q в данной точке поля.
— векторная величина. Она представляет собой силовую характеристику поля, которая определяет силу, действующую на заряд q в данной точке поля. А потенциал φ — скаляр, это энергетическая характеристика поля; он определяет потенциальную энергию заряда q в данной точке поля.