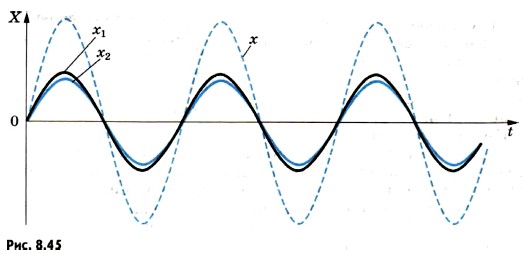
|
|
|
|
|
Глава 8. Световые волны
Интерференция механических волнУсловие максимумовНа рисунке 8.45 изображена зависимость от времени смещений х1 и х2, вызванных двумя волнами при Δd = λ. Разность фаз колебаний равна нулю (или, что то же самое, 2π, так как период синуса равен 2π). В результате сложения этих колебаний возникают результирующие колебания с удвоенной амплитудой. Колебания результирующего смещения х на рисунке показаны цветной штриховой линией. То же самое будет происходить, если на отрезке Δd укладывается не одна, а любое целое число длин волн.
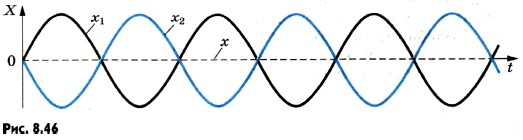
Амплитуда колебаний частиц среды в данной точке максимальна, если разность хода двух волн, возбуждающих колебания в этой точке, равна целому числу длин волн: Δd = ±kλ, (8.14) где k = 0, 1, 2, .... Условие минимумовПусть теперь на отрезке Ad укладывается половина длины волны. Очевидно, что при этом вторая волна отстает от первой на половину периода. Разность фаз оказывается равной л, т. е. колебания будут происходить в противофазе. В результате сложения этих колебаний амплитуда результирующих колебаний равна нулю, т. е. в рассматриваемой точке колебаний нет (рис. 8.46). То же самое произойдет, если на отрезке укладывается любое нечетное число полуволн. Амплитуда колебаний частиц среды в данной точке минимальна, если разность хода двух волн, возбуждающих колебания в этой точке, равна нечетному числу полуволн:
Если разность хода d2 - d1 принимает промежуточное значение между
|
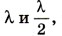то и амплитуда результирующих колебаний принимает некоторое промежуточное значение между удвоенной амплитудой и нулем. Но важно то, что амплитуда колебаний в любой точке не меняется с течением времени. На поверхности воды возникает определенное, неизменное во времени распределение амплитуд колебаний, которое называют интерференционной картиной. На рисунке 8.47 показана фотография интерференционной картины для двух круговых волн от двух источников (черные кружки). Белые участки в средней части фотографии соответствуют максимумам колебаний, а темные — минимумам.
|
|