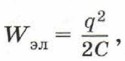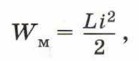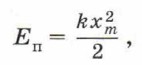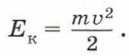Свободные электромагнитные колебания

Превращение энергии в колебательном контуре

2. При зарядке конденсатора ему сообщается энергия

При зарядке конденсатора

где q — заряд конденсатора, С — его ёмкость.

По мере того как конденсатор колебательного контура разряжается, уменьшается энергия его электрического поля, однако за счёт этого растёт энергия магнитного поля катушки:

где L — индуктивность катушки, i — сила тока, протекающего через неё. В момент, когда конденсатор полностью разрядится и его энергия станет равной нулю, энергия магнитного поля катушки станет максимальной и сила тока в этот момент также достигает максимального значения.

Таким образом, в колебательном контуре происходит периодическое превращение энергии электрического поля конденсатора в энергию магнитного поля катушки, и наоборот.

В идеальном колебательном контуре отсутствуют потери энергии, и колебания в нём незатухающие. Для такого контура можно записать закон сохранения энергии:

W_эл + W_м = W = const,

где W — полная энергия контура.

Когда энергия электрического поля максимальна, энергия магнитного поля равна нулю, и наоборот. Поэтому максимальное значение энергии электрического поля равно максимальному значению энергии магнитного поля, и эти значения равны полной энергии контура:

W = W_{эл. m} = W_{м. m}.

Аналогия между механическими и электромагнитными колебаниями

3. Сравним процессы в колебательном контуре с колебаниями пружинного маятника, используя аналогию между механическими и электромагнитными колебаниями.

Вам уже известно: чтобы начались колебания груза пружинного маятника, вначале необходимо деформировать пружину, например сжать. Деформированная пружина будет обладать потенциальной энергией

где х_m — удлинение пружины, или амплитуда.

Процесс деформации пружины аналогичен процессу зарядки конденсатора от источника тока. Следовательно, можно провести аналогию между потенциальной энергией деформированной пружины и энергией электрического поля заряженного конденсатора. Проанализировав эти выражения, можно провести аналогию между жёсткостью пружины k и величиной, обратной ёмкости конденсатора 1/С, а также между удлинением пружины х и зарядом q.

Отпустив сжатую пружину, мы предоставим ей возможность разгонять груз, действуя на него силой упругости. При этом вследствие инертности скорость груза будет нарастать постепенно. Разжимаясь, пружина будет передавать свою энергию грузу, скорость υ которого, а значит, и кинетическая энергия будет возрастать:

Рис.

Анализ выражений кинетической энергии колеблющегося груза и энергии магнитного поля катушки позволяет установить аналогию между массой груза m и индуктивностью катушки L и между скоростью υ и силой тока i.

В системе, состоящей из пружины и груза, происходит периодическое превращение потенциальной энергии деформированной пружины в кинетическую энергию груза и наоборот, аналогично тому, как периодически превращаются друг в друга энергия электрического поля конденсатора и энергия магнитного поля катушки в колебательном контуре. Можно говорить об аналогии электромагнитных и механических колебаний, рассматривая не пружинный маятник, а любую другую механическую систему, например математический маятник: выводы от этого не изменятся.

С учётом проведённой аналогии можно записать уравнение зависимости заряда и силы тока от времени:

q = q_mcos ωt, i = -I_msin ωt, при этом I_m = q_mω.

Таким образом, колебания заряда и силы тока в контуре являются гармоническими.

<<< К началу Окончание >>>