|
|
|
|
|
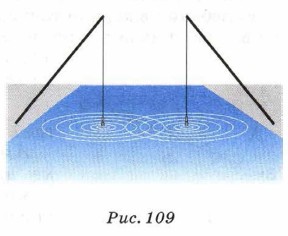
Глава 4. Оптика § 29. Интерференция светаИнтерференция волн1. Явление интерференции вам знакомо из курса физики основной школы. Рассмотрим это явление подробнее. Интерференцию механических волн можно наблюдать, например, на поверхности воды, если поблизости колеблются два одинаковых поплавка (рис. 109).
Каждый из них является источником волн, которые свободно проходят одна сквозь другую, не изменяясь при этом. Если посмотреть более внимательно, то можно заметить, что на одних участках поверхности, где волны накладываются, они усиливают друг друга, на других же участках, напротив, — ослабляют. Образующуюся на поверхности воды картину называют интерференционной.
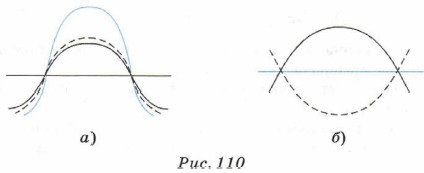
Понять причину интерференции достаточно просто: в каждой точке, где происходит наложение волны, складываются их колебания. Если говорить о волнах на поверхности воды, то усиливаются волны в тех точках, где встречаются их гребни (рис. 110, а). Ослабляются же волны там, где гребень одной из них встречается со впадиной другой (рис. 110, б).
Когерентность. Условия максимумов и минимумов2. Устойчивая интерференционная картина наблюдается лишь при условии когерентности.
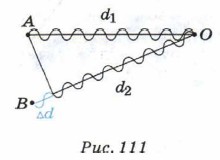
Волны, созданные такими источниками, называют когерентными. Определим условия, при которых в той или иной точке пространства наблюдается усиление или ослабление колебаний, или, как принято говорить, условие максимумов и условие минимумов. Будем рассматривать случай, когда разность фаз колебаний двух источников равна нулю. От источников А и В до данной точки О пространства волны проходят разные расстояния d1 и d2 (рис. 111) и, таким образом, имеют разность хода Δd = d2 - d1.
Колебания в данной точке пространства будут усиливаться, если волны приходят в неё в одинаковой фазе. Такое возможно, если на участке Δd укладывается целое число длин волн. Это условие максимумов: Δd = kλ, где λ — длина волны, k = 0; 1; 2; ... . Амплитуда колебаний в данной точке пространства максимальна, если разность хода волн составляет целое число длин волн. Если в данную точку пространства волны приходят в противофазе, то амплитуда результирующего колебания получается минимальной. На отрезке Δd укладывается при этом нечётное число полуволн. Это условие минимумов: Δd = (2k + 1)λ/2, где k = 0; 1; 2; ... . Амплитуда колебаний в данной точке пространства минимальна, если разность хода волн составляет нечётное число полуволн. Отметим, что энергия волн при интерференции перераспределяется в пространстве: энергия концентрируется в максимумах, в то время как в минимумы не поступает совсем.
|
|
|