|
|
|
|
|
Глава 5. Основы специальной теории относительности § 34. Представления классической физики о пространстве и времени (окончание)Так, в соответствии с первым законом Ньютона тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока на него не действуют другие тела. Таким образом, покой и равномерное прямолинейное движение равноправны. Второй закон Ньютона также не противоречит принципу относительности Галилея, поскольку в классической механике масса тела, действующая на него сила и его ускорение — величины инвариантные. Преобразования Галилея6. Рассмотрим уравнения преобразования координат при переходе от одной системы отсчёта к другой. Пусть система отсчёта К' движется относительно системы К со скоростью Через промежуток времени t: х' = x0 - υt, у' = y,z' = z, t' = t. Записанные формулы называют преобразованиями Галилея. Они связывают координаты и время в двух инерциальных системах отсчёта. Вопросы для самопроверки 1. Каковы свойства пространства и времени в классической физике? Поясните эти свойства на примерах. 2. Что составляет систему отсчёта? В чём отличие инерциальной системы отсчёта от неинерциальной? 3. Сформулируйте классический закон сложения скоростей. 4. Какие величины, характеризующие механическое движение и взаимодействие тел в механике, являются относительными; инвариантными? 5. Как читается принцип относительности Галилея? Упражнение 26 1. Пользуясь преобразованиями Галилея, покажите, что расстояние между двумя точками не изменяется при переходе от одной инерциальной системы отсчёта к другой. 2. Пользуясь преобразованиями Галилея, докажите инвариантность ускорения. 3. Получите из преобразований Галилея классический закон сложения скоростей. 4. Получите формулы преобразования координат при переходе от движущейся системы отсчёта к неподвижной.
|
|
|



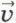 , направленной вдоль оси X (см. рис. 125). В начальный момент времени
, направленной вдоль оси X (см. рис. 125). В начальный момент времени 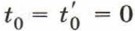 начала координат — точки О и О' — совпадают, т. е.
начала координат — точки О и О' — совпадают, т. е.