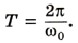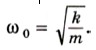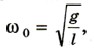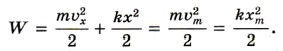|
|
|
|
|
Глава 3. Механические колебания Примеры решения задач. Упражнение 3. Краткие итоги главы 3Примеры решения задач1. Сколько колебаний совершает математический маятник длиной l = 4,9 м за время t = 5 мин? Р е ш е н и е. Период колебаний определяется по формуле
Искомое число колебаний можно найти так:
2. Вертикально подвешенная пружина растягивается прикрепленным к ней грузом на Δl = 0,8 см. Чему равен период Т свободных колебаний груза? (Массой пружины пренебречь.) Р е ш е н и е. Период колебаний груза, прикрепленного к пружине, определяется формулой
где m — масса груза; k — жесткость пружины. На груз действуют сила тяжести FT = Fynp. Так как FT = mg и Fynp = k Δl (закон Гука), то mg = kΔl, откуда Следовательно,
3. На горизонтальном стержне находится груз, прикрепленный к пружине (см. рис. 3.3). Другой конец пружины закреплен. В некоторый момент времени груз смещают от положения равновесия на хm = 10 см и отпускают. Определите координату груза спустя 1/8 периода колебаний. (Трение не учитывать.) Р е ш е н и е. Зависимость координаты груза от времени выражается так: x = xm cos ω0t.
4. Груз, прикрепленный к пружине, колеблется на горизонтальном гладком стержне (см. рис. 3.3). Определите отношение кинетической энергии груза к потенциальной энергии системы в момент, когда груз находится в точке, расположенной посредине между крайним положением и положением равновесия. Р е ш е н и е. Координата указанной точки равна половине амплитуды колебаний:
В любой момент времени выполняется равенство
Поэтому кинетическая энергия груза в момент прохождения им указанной точки определяется так:
Упражнение 31. Груз массой 100 г совершает колебания с частотой 2 Гц под действием пружины. Определите жесткость пружины. 2. В Санкт-Петербурге в Исаакиевском соборе висел маятник Фуко, длина которого была равна 98 м. Чему был равен период колебаний маятника? 3. Шарик на пружине сместили на расстояние 1 см от положения равновесия и отпустили. Какой путь пройдет шарик за 2 с, если частота его колебаний ν = 5 Гц? (Затуханием колебаний можно пренебречь.) 4. Тело массой 200 г совершает колебания в горизонтальной плоскости с амплитудой 2 см под действием пружины жесткостью 16 Н/м. Определите циклическую частоту колебаний тела и энергию системы. 5. Автомобиль движется по неровной дороге, на которой расстояние между буграми приблизительно равно 8 м. Период свободных колебаний автомобиля на рессорах 1,5 с. При какой скорости автомобиля его колебания в вертикальной плоскости станут особенно заметными? Краткие итоги главы 31. Колебания различной природы (механические, электрические и др.) описываются одинаковыми уравнениями. Различают свободные, затухающие и вынужденные колебания. 2. Свободные колебания возникают в системе под влиянием внутренних сил после того, как она выведена из состояния равновесия. С течением времени свободные колебания вследствие трения затухают. 3. Вынужденные колебания возникают при действии на систему внешней периодической силы. Эти колебания не затухают до тех пор, пока действует внешняя сила. Пример вынужденных колебаний: раскачивание качелей с помощью периодических толчков. 4. Свободные колебания груза, прикрепленного к пружине, можно описать вторым законом Ньютона. Его следствием применительно к данному случаю является уравнение
где х — смещение груза от положения равновесия; х" — ускорение груза; 5. Решение уравнения, описывающего свободные колебания, выражается через косинус: х = хm cos (ω0t + φ0) — или синус. Колебания, происходящие по закону косинуса или синуса, называются гармоническими. 6. Модуль максимального смещения тела хm от положения равновесия называется амплитудой колебаний. Величина ω0 называется циклической частотой колебаний и выражается через частоту колебаний ν так: ω0 = 2πν. 7. Промежуток времени, за который система совершает одно полное колебание, называется периодом колебаний. Период можно выразить через циклическую частоту:
8. Величину, стоящую под знаком косинуса или синуса, называют фазой колебаний. Фаза определяет положение колеблющегося тела в произвольный момент времени при заданной амплитуде колебаний. 9. Собственная циклическая частота колебаний груза, прикрепленного к пружине, зависит от его массы m и жесткости пружины k:
Собственная циклическая частота колебаний математического маятника определяется формулой
где g — ускорение свободного падения, а l — длина маятника. Частота (как и период) гармонических колебаний не зависит от амплитуды. 10. Энергия колеблющегося тела при отсутствии сил трения сохраняется:
Вынужденные колебания совершаются при воздействии на систему, в которой могут происходить колебания, периодической силы. При этом может наблюдаться резонанс: резкое возрастание амплитуды вынужденных колебаний при совпадении частоты изменения внешней силы с собственной частотой колебаний системы. Резонанс проявляется отчетливо лишь в системах с малым трением.
|
|
|



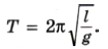
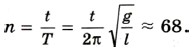
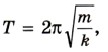
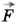 T и сила упругости
T и сила упругости 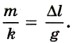
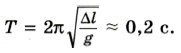
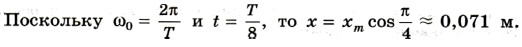
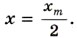 Потенциальная энергия системы в момент прохождения груза через эту точку равна:
Потенциальная энергия системы в момент прохождения груза через эту точку равна:
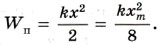
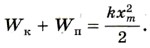
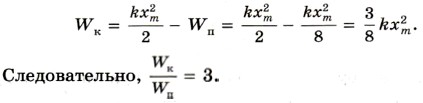
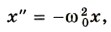
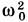 — постоянная, зависящая от свойств системы.
— постоянная, зависящая от свойств системы.