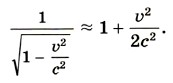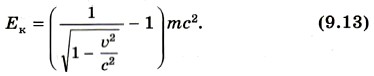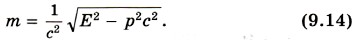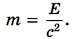|
|
|
|
|
Глава 9. Элементы теории относительности § 79. Элементы релятивистской динамикиС новыми пространственно-временными представлениями не согласуются при больших скоростях движения и законы механики Ньютона. Лишь при малых скоростях движения, когда справедливы классические представления о пространстве и времени, второй закон Ньютона (уравнение движения)
не меняет своей формы при переходе от одной инерциальной системы отсчета к другой (выполняется принцип относительности). Но при больших скоростях движения этот закон в своей обычной (классической) форме несправедлив. Однако введенные в динамике основные понятия: энергия, импульс — имеют тот же физический смысл, лишь понятие массы в классической механике отличается от понятия массы в релятивистской динамике. В природе существуют частицы, скорость которых равна скорости света. Это фотоны и различного типа нейтрино. Масса этих частиц равна нулю. Они не могут быть замедлены или ускорены. Поэтому во всех инерциальных системах отсчета их импульс и энергия не равны нулю. Такие частицы называются безмассовыми. Энергия и импульс таких частиц связаны соотношениями Е = рс и Е2 - р2с2 = 0. (9.5) Эти соотношения экспериментально подтверждены. Однако для большинства частиц масса является одной из важнейших характеристик. Эти частицы называются массовыми. Скорость таких частиц υ < с. Массовая частица обладает собственной энергией: Е = mс2. (9.6) Согласно этой формуле тело обладает энергией и при скорости, равной нулю — энергией покоя. Это замечательный результат. Любое тело уже только благодаря факту своего существования обладает энергией, которая пропорциональна его массе m. При превращениях элементарных частиц, обладающих массой покоя m ≠ 0, в частицы, у которых m = 0, их энергия покоя Е0 целиком превращается в кинетическую энергию вновь образовавшихся частиц. Этот факт является наиболее очевидным экспериментальным доказательством существования энергии покоя. Во всех инерциальных системах отсчета импульс частицы и ее энергия связаны соотношением: Е2 - р2с2 = m2с4. (9.7) Так как величины m и с не меняются при переходе от одной системы отсчета к другой, то, следовательно, не меняется и значение Е2 - р2с2. Выражение (9.7) преобразуется в уравнение (9.5) при m = 0, следовательно, оно справедливо также и для безмассовых частиц. Формула (9.7) является фундаментальным соотношением релятивистской механики. Энергия частицы выражается через ее импульс следующим образом:
Используя формулу (9.8), а также учитывая, что импульс частицы пропорционален ее скорости и энергии, получаем выражения для импульса и энергии частицы:
При υ « с мы получим выражение для импульса в классической механике: Множитель при малых скоростях можно преобразовать:
Подставив это выражение в формулу (9.10) и получим
Последнее слагаемое — это выражение для кинетической энергии в классической механике. Первое слагаемое в формуле (9.11) — это собственная энергия частицы. Релятивистская энергия есть сумма собственной энергии частицы и релятивистской кинетической энергии Ек: Е = mс2 + Ек. (9.12) Из уравнений (9.10) и (9.12) получим выражение для релятивистской кинетической энергии массовой частицы
Заметим, что если υ → с, то Ек → ∞, что невозможно. Это означает, что скорость массовой частицы всегда меньше скорости света. Масса частицы из формулы (9.8) имеет вид:
Если частица покоится, то Обратим внимание на то, что так как подкоренное выражение в формуле (9.14) не зависит от выбора системы отсчета, то масса частицы не зависит от ее движения и остается одной и той же величиной во всех инерциальных системах отсчета. Принцип соответствия. Законы динамики Ньютона и классические представления о пространстве и времени можно рассматривать как частный случай релятивистских законов при скоростях движения, много меньших скорости света. Это проявление так называемого принципа соответствия, согласно которому любая теория, претендующая на более глубокое описание явлений и на более широкую сферу применимости, чем старая, должна включать последнюю как предельный случай. Принцип соответствия впервые был сформулирован Нильсом Бором применительно к связи квантовой и классической теорий. Импульс частицы и ее энергия зависят от выбора системы отсчета, масса же всегда остается постоянной. При скоростях много меньших скорости света релятивистские выражения для импульса и энергии переходят в выражения классической механики (принцип соответствия). Вопросы к параграфу 1. Какие величины не изменяются при переходе от одной инерциальной системы отсчета к другой? 2. Какие частицы могут двигаться со скоростью света? 3. В чем состоит принцип соответствия?
|
|
|




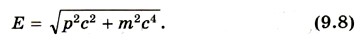
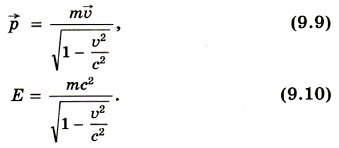
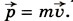
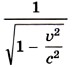 (релятивистский множитель)
(релятивистский множитель)