|
|
|
|
|
Глава 4. Работа и мощность. Энергия § 58. Рычаг. Равновесие сил на рычагеРассмотрим самый простой и распространённый механизм — рычаг.
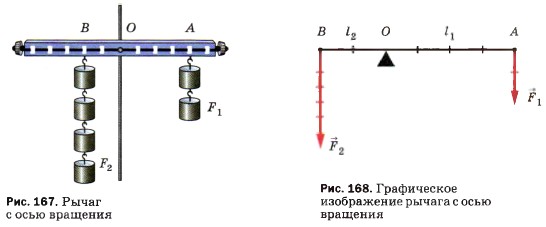
Рычаг представляет собой твёрдое тело, которое может вращаться вокруг неподвижной опоры. На рисунке 164 показано, как рабочий для поднятия груза использует в качестве рычага лом. В первом случае рабочий с силой F нажимает на конец лома В, во втором — приподнимает конец В. Рабочему нужно преодолеть вес груза Р — силу, направленную вертикально вниз. Он поворачивает для этого лом вокруг оси, проходящей через единственную неподвижную точку лома — точку его опоры О. Сила F, с которой рабочий действует на рычаг, меньше силы Р, таким образом, рабочий получает выигрыш в силе. При помощи рычага можно поднять такой тяжёлый груз, который без рычага поднять нельзя. На рисунке 167 изображён рычаг, ось вращения которого О (точка опоры) расположена между точками приложения сил А и В. На рисунке 168 показана схема этого рычага. Обе силы F1 и В2, действующие на рычаг, направлены в одну сторону.
Чтобы найти плечо силы, надо из точки опоры опустит перпендикуляр на линию действия силы.
Длина этого перпендикуляра и будет плечом данной силы. На рисунке 168 показано, что О А — плечо силы F1; ОВ — плечо силы F2. Силы, действующие на рычаг, могут повернуть его вокруг оси в двух направлениях: по ходу или против хода часовой стрелки. Так, сила F1 (см. рис. 167) вращает рычаг по ходу часовой стрелки, а сила F2 вращает его против хода часовой стрелки. Условие, при котором рычаг находится в равновесии под действием приложенных к нему сил, можно установить на опыте. При этом надо помнить, что результат действия силы зависит не только от её числового значения (модуля), но и от того, в какой точке она приложена к телу и как направлена. К рычагу (см. рис. 167) по обе стороны от точки опоры подвешивают различные грузы так, чтобы рычаг каждый раз оставался в равновесии. Действующие на рычаг силы равны весам этих грузов. Для каждого случая измеряют модули сил и их плечи. Из опыта, изображённого на рисунке 167, видно, что сила 2 Н уравновешивает силу 4 Н. При этом, как видно из рисунка, плечо меньшей силы в 2 раза больше плеча большей силы. На основании таких опытов было установлено условие (правило) равновесия рычага.
Это правило можно записать в виде формулы
где F1 и F2 — силы, действующие на рычаг, Правило равновесия рычага было установлено Архимедом около 287—212 гг. до н. э. Из этого правила следует, что меньшей силой можно уравновесить при помощи рычага большую силу. Пусть одно плечо рычага в 2 раза больше другого (см. рис. 167). Тогда, прикладывая в точке А силу, например, в 400 Н, можно в точке В уравновесить рычаг силой, равной 800 Н. Чтобы поднять ещё более тяжёлый груз, нужно увеличить длину плеча рычага, на которое действует рабочий. П р и м е р. С помощью рычага рабочий поднимает каменную глыбу массой 240 кг (см. рис. 164). Какую силу прикладывает он к большему плечу рычага, равному 2,4 м, если меньшее плечо равно 0,6 м? Запишем условие задачи и решим её.
В нашем примере рабочий преодолевает силу 2400 Н, прикладывая к рычагу силу 600 Н. Он получает выигрыш в силе в 4 раза. Но при этом плечо, на которое действует рабочий, в 4 раза длиннее того, на которое действует вес плиты ( Применяя правило рычага, можно меньшей силой уравновесить большую силу. При этом плечо меньшей силы должно быть длиннее плеча большей силы. Вопросы1. Что представляет собой рычаг?
|
|
|




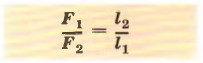
 1 и
1 и 